


Next: Learning and retrieval
Up: ReST model
Previous: Spontaneous dynamics
Predictability
Only the primary layer is stimulated by a spatio-temporal input
signal. The input signal is supposed sparse, and parameter
 denotes the input sparsity (the average proportion of
neurons which are stimulated at each time). As the number of
primary neurons is equal to the number of input channels, the
activation signals of primary neurons are strongly correlated with
their input signals. If we suppose moreover that the input signal
is binary, i.e.
denotes the input sparsity (the average proportion of
neurons which are stimulated at each time). As the number of
primary neurons is equal to the number of input channels, the
activation signals of primary neurons are strongly correlated with
their input signals. If we suppose moreover that the input signal
is binary, i.e.
 ,
the primary pattern of activation
,
the primary pattern of activation
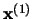 and the
input signal
and the
input signal
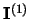 have almost the same values. On
the contrary, there is no spatial matching between the primary
pattern of activation
have almost the same values. On
the contrary, there is no spatial matching between the primary
pattern of activation
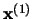 (and/or the input signal
(and/or the input signal
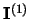 ) and the secondary pattern of activation
) and the secondary pattern of activation
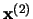 .
.
Figure 2:
Measures of correlations between spatial patterns of
activation, in primary and secondary layers, for (random)
non-periodic and periodic input signals. The activity of the
system is observed between  and
and  . For
. For
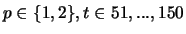 , we measure the correlation between
, we measure the correlation between
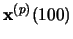 and
and
 .
.  ,
,
 , other parameters are in Tab.1. - a - Non-periodic input signal, Primary layer, - b -
Non-periodic input signal, Secondary layer, - c - Period-5
input signal, Primary layer, - d - Period-5 input signal,
Secondary layer.
, other parameters are in Tab.1. - a - Non-periodic input signal, Primary layer, - b -
Non-periodic input signal, Secondary layer, - c - Period-5
input signal, Primary layer, - d - Period-5 input signal,
Secondary layer.
|
|
One can however remark that primary and secondary patterns of activation
are not independent (due to the weights couplings between
the two layers). In other words, the dynamics that takes place in secondary
layer is partly predictable, knowing primary layer activity.
This statistical dependency can be observed if our system is submitted to a
periodic input signal
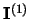 of period
of period
 so that
so that
 (see Fig.2).
In that case, the
chaotic dynamics in the secondary layer has a residual
periodicity, i.e.
(see Fig.2).
In that case, the
chaotic dynamics in the secondary layer has a residual
periodicity, i.e.
 . This mutual periodicity makes it possible to associate the
periodic primary pattern of activation
. This mutual periodicity makes it possible to associate the
periodic primary pattern of activation
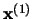 to the
periodically distributed secondary pattern of activation
to the
periodically distributed secondary pattern of activation
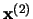 (comparable to a cyclo-stationary random process).
So, in case of periodic input
signals, primary and secondary layers display a
weak dynamical coupling, i.e. one
can predict the distribution of secondary layer activations, knowing
the primary pattern of activation. This statistical predictability
allows to learn
spatio-temporal associations between the two layers, and will be
used in next section.
Note however that secondary layer chaotic dynamics is not equivalent to
(and richer than) a random process.
Indeed, we have remarked that the distribution of activations in the
secondary layer is highly sensitive to small changes on the
spatial and temporal characteristics of the input signal.
One can observe a strong remapping in the secondary pattern of activation
after a little change on the input signal.
This denotes a structural instability of the dynamics
(a spontaneous tendency to modify its inner dynamical organization).
Our system is thus highly sensitive to noise or stimulus
variations.
It thus behaves in a very different manner than a system
composed of stochastic units.
We have also remarked that signals with
long periods (i.e.
(comparable to a cyclo-stationary random process).
So, in case of periodic input
signals, primary and secondary layers display a
weak dynamical coupling, i.e. one
can predict the distribution of secondary layer activations, knowing
the primary pattern of activation. This statistical predictability
allows to learn
spatio-temporal associations between the two layers, and will be
used in next section.
Note however that secondary layer chaotic dynamics is not equivalent to
(and richer than) a random process.
Indeed, we have remarked that the distribution of activations in the
secondary layer is highly sensitive to small changes on the
spatial and temporal characteristics of the input signal.
One can observe a strong remapping in the secondary pattern of activation
after a little change on the input signal.
This denotes a structural instability of the dynamics
(a spontaneous tendency to modify its inner dynamical organization).
Our system is thus highly sensitive to noise or stimulus
variations.
It thus behaves in a very different manner than a system
composed of stochastic units.
We have also remarked that signals with
long periods (i.e.  ) lead to a
secondary pattern of activation whose residual
period is an harmonic of the input period. In that case,
one can not
have bijective associations between primary spatial patterns of
activation and secondary spatial distributions of activation.
In next sections, we assume that input sequences have rather short
periods, of the order of 3-10.
) lead to a
secondary pattern of activation whose residual
period is an harmonic of the input period. In that case,
one can not
have bijective associations between primary spatial patterns of
activation and secondary spatial distributions of activation.
In next sections, we assume that input sequences have rather short
periods, of the order of 3-10.



Next: Learning and retrieval
Up: ReST model
Previous: Spontaneous dynamics
Dauce Emmanuel
2003-04-08
![\includegraphics[width=8cm]{bc_cross_corr.eps}](img123.png)
![\includegraphics[width=8cm]{bc_cross_corr.eps}](img123.png)