Dans le cadre de la mise en place d'un circuit d'activation à la déstabilisation, il reste la question du choix précis des neurones : dans quelle mesure la matrice des poids détermine-t-elle la position d'un neurone au sein du circuit? On va voir dans le paragraphe suivant que la contrainte des poids est beaucoup plus lâche que dans le cas de la configuration spatiale, mais on peut néanmoins la mettre en évidence en utilisant la notion de frustration.
Dans un premier temps, on définit la covariance croisée selon le délai ![]() , qui nous servira au paragraphe suivant pour caractériser la frustration.
, qui nous servira au paragraphe suivant pour caractériser la frustration.
Étant donnés deux signaux ![]() et
et ![]() , de moyenne
, de moyenne 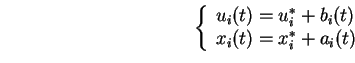 et
et  , pour
, pour ![]() de 1 à
de 1 à ![]() , l'expression empirique de leur covariance selon le délai
, l'expression empirique de leur covariance selon le délai ![]() est donnée par :
est donnée par :
Dans le cadre de notre modèle, on s'intéressera essentiellement au délai 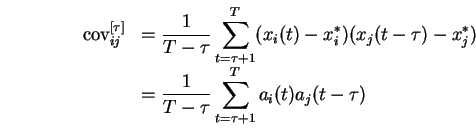 , qui donne le délai de transmission.
Dans ce cas, la covariance entre
, qui donne le délai de transmission.
Dans ce cas, la covariance entre ![]() et
et ![]() donne une indication sur les rapports de succession dans la transmission de l'activité dynamique.
Une valeur positive de la covariance indique que le signal afférent du neurone
donne une indication sur les rapports de succession dans la transmission de l'activité dynamique.
Une valeur positive de la covariance indique que le signal afférent du neurone ![]() est synchronisé avec le signal efférent du neurone
est synchronisé avec le signal efférent du neurone ![]() .
Une valeur négative indique que le neurone
.
Une valeur négative indique que le neurone ![]() produit un signal afférent en opposition avec le signal efférent du neurone
produit un signal afférent en opposition avec le signal efférent du neurone ![]() .
Si cette valeur est proche de zéro, les signaux peuvent être considérés comme non-corrélés, un cas fréquent de non-corrélation correspondant au fait que l'un au moins des neurones est figé.
.
Si cette valeur est proche de zéro, les signaux peuvent être considérés comme non-corrélés, un cas fréquent de non-corrélation correspondant au fait que l'un au moins des neurones est figé.