Circuits d'activation, dynamique pseudo-périodique

Considérons un réseau en régime cyclique (périodique ou pseudo-périodique), présentant une période dominante $\tau$.

Si la période est entière, elle représente le nombre de pas de temps nécessaires pour que la dynamique s'auto-reproduise. Le réseau passe par $\tau$ états distincts avant de revenir à son point de départ et de recommencer le cycle. On voit donc bien dans ce cas qu'il existe une séquence d'états $x(t)$, $t=1..\tau$, qui caractérise complètement la dynamique.

Dans le cas générique d'un régime pseudo-pérodique, on peut tenir un raisonnement analogue, et dire que la pseudo-période nous donne une valeur approchée du nombre de pas de temps nécessaires pour revenir dans un état voisin de l'état dans lequel a débuté le cycle.

Pour une dynamique de type chaotique présentant une périodicité résiduelle, les maxima de l'autocorrélogramme nous donnent la même estimation du temps au bout duquel la dynamique tend à s'auto-reproduire. On conçoit que plus le chaos est profond, moins cette reproduction est fidèle.

Étant donnés $N$ signaux $\{x_i(t)\}_{i=1..N,t=1..T}$, la matrice des variances-covariances est donnée par :

cov$$_{ij}=\frac{1}{T}\sum_{t=1}^T (x_i(t)-x_i^*)(x_j(t)-x_j^*)$$

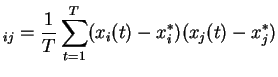où $\bar{x}_i$ représente la moyenne empirique du signal $x_i(t)$ et la matrice des corrélations croisées est obtenue par normalisation de la matrice des variances-covariances, soit :

$$\psi_{ij}=\frac{\mbox{cov}_{ij}}{\sigma_{x_i}\sigma_{x_j}}$$

où $\sigma_{x_i}$ et $\sigma_{x_j}$ sont les écarts-types des signaux $x_i(t)$ et $x_j(t)$.

On se place sur un réseau de taille $N=200$, en dynamique pseudo-périodique, avec une pseudo-période proche de 6 ( $\tau \simeq 5.88$). Dans ces conditions, on considère que les neurones pour lesquels $\psi_{ij}$ est proche de 1 sont synchronisés. Ceux pour lesquels $\psi_{ij}$ est proche de -1 sont considérés en opposition de phase.

On a représenté sur la partie gauche de la figure 3.11 une partie de matrice des corrélations croisées, correspondant aux signaux d'activation émis par les 40 premiers neurones du réseau. On a représenté sur la partie droite de la figure 3.11 la même matrice, dont on a permuté les lignes et les colonnes en fonction de la ressemblance entre ces lignes et ces colonnes. Ce classement permet de mettre en relief les caractéristiques communes de certaines lignes et de certaines colonnes ; on met ainsi côte à côte les indices des signaux dont les valeurs de corrélation croisées présentent la même configuration.

Figure 3.11: Matrice des corrélations croisées. À gauche : matrice de corrélations croisées pour les 40 premiers signaux d'activation. À droite : la même matrice dont on a classé les lignes et les colonnes pour faire ressortir les neurones dont les signaux d'activation ont des caractéristiques communes. Représentation de Hinton. Paramètres : $g=7.6$ (régime cyclique), $T=100$, $N=200$, $\bar{\theta}=0.1$, $\sigma _\theta =0.1$, $\bar{J}=0$, $\sigma _J=1$

On voit sur la matrice classée la présence de blocs sur la diagonale, dont les frontières sont plus ou moins bien délimitées. Le fait de raisonner sur des ``blocs'' permet juste de fixer les idées dans un premier temps.

Les neurones appartenant au même bloc tendent à être mutuellement synchronisés. La corrélation étant proche de 1, tous les neurones de ce bloc produisent un signal qui a les mêmes caractéristiques.

Qui plus est, ce bloc peut être mis en correspondance avec un bloc négatif à valeurs proche de -1, situé dans le même alignement. Le signal produit par les neurones du deuxième bloc semble donc avoir les mêmes caractéristiques, à ceci près qu'il est décalé dans le temps d'une demi-période.

On a représenté sur la figure 3.12 des signaux individuels issus du même réseau présentant deux à deux un décalage de phase de 1 (on repère la valeur de ce décalage de phase par rapport à l'instant où la dérivée du signal s'annule).

Figure 3.12: Quelques signaux individuels en décalage de phase. On a représenté six signaux individuels pris dans un réseau en régime pseudo-périodique, présentant deux à deux un décalage de phase de 1. Paramètres : $g=7.6$, $T=40$, $N=200$, $\bar{\theta}=0.1$, $\sigma _\theta =0.1$, $\bar{J}=0$, $\sigma _J=1$

On voit bien sur la figure 3.12 que le signal d'activation du premier neurone ($i=140$) est corrélé à celui du second neurone ($j=25$) au pas de temps précédent. Ceci est vrai pour tout temps en moyenne. On a le même rapport de corrélation entre l'activation du second neurone au temps $t$ et celle du troisième au temps $t-1$, quel que soit $t$. De proche en proche, on voit que l'on peut établir un circuit d'activation qui propage un signal en boucle fermée du sixième au premier neurone.

Par extension, tout neurone en phase avec le deuxième neurone propage le même signal vers tout neurone en phase avec le premier neurone. On voit donc que ce circuit d'activation met en jeu tous les neurones du réseau, qui servent de relais pour la propagation en boucle fermée du même signal dynamique. Le nombre de relais est en moyenne égal à la période interne de la dynamique.

Figure 3.13: Circuit d'activation, période $\tau$.

Plusieurs raisons font que l'appartenance à une classe (une étape du circuit) n'est pas absolue, mais obéit à des critères flous. Tout d'abord, même en régime cyclique, il y a des signaux dont les harmoniques sont prépondérants par rapport à la fréquence fondamentale, et qui présentent deux maxima sur l'intervalle d'une période. Ils appartiennent dans ce cas à deux classes en opposition de phase. Par ailleurs, le décalage de phase entre deux neurones est lui même non-entier, et il existe des neurones qui se positionnent de façon intermédiaire entre deux classes successives. Enfin, lorsque la période est non entière, le nombre de classes lui même peut être approximé par la valeur entière la plus proche, mais on peut aussi considérer que le nombre de classes est fractionnaire.

Malgré toutes ces remarques, il y a une structure qui émerge de l'activité dynamique, qui permet dans les faits de différencier fonctionnellement les neurones par leur appartenance à une (ou plusieurs) étapes du circuit. Les neurones sont placés dans un rapport de succession temporelle. On parle dans ce cas de configuration dynamique (par opposition à configuration spatiale). Seule l'observation des signaux d'activation permet de définir le circuit. Ce circuit manifeste une architecture dont les caractéristiques ne sont pas directement déductibles des valeurs de la matrice des poids.

C'est plutôt sur une toute autre propriété de la matrice des poids que repose la mise en place de ce circuit. La matrice des poids est en effet une matrice aléatoire de grande taille. Ces deux caractéristiques : aléatoire et de grande taille sont importantes. C'est en effet en raisonnant sur le comportement limite des systèmes aléatoires de grande taille que l'on peut proposer une explication sur la mise en place de ce circuit.

Les équations de champ moyen (voir page ) décrivent un processus itératif sur les grandeurs macroscopiques du système (moyenne $m(t)$, moment du deuxième ordre $q(t)$). Ce processus permet de déterminer l'évolution de ces grandeurs en fonction de la loi initiale des activations. Sur le modèle à une population, la valeur moyenne $m(t)$ tend vers une constante $m^*$, quel que soit le régime décrit (point fixe ou chaos). Cela signifie en particulier que dans le cas du régime chaotique, l'activité de tous les neurones se compense en moyenne. Autrement dit : les neurones ne sont pas synchronisés.

Comme on l'a vu, à taille finie, sur un intervalle de temps $1..T$, la valeur empirique moyenne $m_N(t)$ est d'autant plus proche de la moyenne théorique des ECM $m(t)$ que la taille est élevée. En particulier, dans la mesure où $m(t)$ se rapproche de son point fixe $m^*$ pour $t$ grand (numériquement : $t>10$, voir figure 2.2), $m_N(t)$ tend également à être constant et proche de $m^*$ pour les $t$ et les $N$ grands (voir aussi page ). La diminution de l'écart-type du signal moyen est assez lente (en $1/\sqrt {N}$) comme on peut le constater sur la figure 2.14. Néanmoins, pour des tailles à partir de $N=50$, l'écart-type du signal moyen est déjà très significativement inférieure à la moyenne des écarts-types des signaux individuels.

Cette absence de synchronisation est indépendante du régime dynamique qui se développe dans le réseau. Elle est assez banale si on considère un régime chaotique profond, où les signaux individuels ressemblent à du bruit décorrélé. Par contre, pour des régimes périodiques ou pseudo-périodiques, la décorrélation des signaux individuels implique que les phases individuelles soient uniformément réparties sur $[0,\tau]$, où $\tau$ est la valeur de la période ou pseudo-période.

Une petite simulation simplificatrice montre que cette conséquence aboutit naturellement à la mise en place de circuits d'activation. On condsidère $N$ signaux dont le décalage de phase est compris entre $\frac{\tau}{N}$ et $\tau$ : pour $i=1..N$, $\tilde{u}_i(t)=0.3*\sin(\frac{\pi}{3}t+\frac{i}{2\pi N})-0.4$. Ces signaux ont des caractéristiques (moyenne, écart-type) que l'on peut retrouver sur un réseau réel. On a représenté ce signal sur la figure 3.14, ainsi que sa matrice de corrélations.

Figure 3.14: 30 signaux périodiques de période 6 dont la phase est uniformément répartie et matrice de corrélations associée.

La matrice de corrélation associée à ces signaux ne permet pas de déceler des blocs distincts caractérisant des signaux manifestant mutuellement un degré de corrélation élevé (ou du moins l'élaboration de telles classes serait purement arbitraire).

Si l'on fait passer ces signaux par la fonction de transfert $f_g$, on constate que la déformation du signal induite a pour effet d'associer les maxima d'activation à des instants discrets, et donc finalement de créer des classes de neurones qui tendent à atteindre leur maximum (sous forme de pic d'activation) simultanément. Des blocs apparaissent alors sur la diagonale (voir figure 3.15) qui ont pour effet de séparer fonctionnellement les neurones, et de faire apparaître les différentes étapes du circuit. On peut également voir dans ce cas que l'appartenance à une classe est floue, dans la mesure où il reste des neurones qui sont intermédiaires entre deux classes.

Figure 3.15: Passage par la fonction de transfert ($g=8$) des signaux précédents, et matrice de corrélations associée.

Ce phénomène, observé sur des signaux très simples, est également à l'uvre sur les réseaux que nous étudions, même si les signaux sont moins réguliers. L'apparition des circuits d'activation repose à la fois sur une contrainte forte de non synchronisation entre les neurones, sur la présence de régimes cycliques à taille finie et sur les caractéristiques non-linéaires de la fonction de transfert.

Le nombre d'étapes du circuit repose évidemment sur la période initiale, qui elle-même provient des valeurs propres de la jacobienne à la déstabilisation. La configuration spatiale a donc une influence directe sur les caractéristiques du circuit.

Sachant que la probabilité d'apparition d'une période longue est plus faible que celle d'une période courte, et que le circuit d'activation qui se met en place possède $\tau$ étapes, on voit en conséquence que les circuits longs sont moins probables que les circuits courts. C'est bien les circuits les plus ``simples'' qui sont favorisés de façon générale.

La mise en évidence de circuits d'activations sur un régime cyclique a taille finie est une illustration intéressante de la contrainte exercée par le macroscopique sur le microscopique. On voit en effet que les régimes cycliques, qui ne sont pas décrits à la limite thermodynamique, subissent néanmoins la contrainte de décorrélation des signaux individuels mise en évidence à la limite thermodynamique. Cette contrainte implique, pour ces régimes cycliques, que les phases des signaux individuels soient uniformément réparties sur la longueur de la période, ce qui a pour conséquence de faire émerger une structure dynamique en forme de circuit qui propage la phase d'un groupe de neurones à l'autre.

Par analogie avec la configuration spatiale (neurones muets/actifs/saturés), on a parlé de configuration dynamique pour désigner ce circuit. Cette nouvelle forme d'organisation permet de classer les neurones selon leur phase, indépendamment de l'amplitude de leur signal.

Les paragraphes qui suivent tentent d'évaluer dans quelle mesure la configuration dynamique peut être déduite des couplages $J_{ij}$, et montre également la relative indépendance de la structure du circuit par rapport à une augmentation du paramètre de gain $g$ et à une complexification de la dynamique.