Les équations de champ moyen (ECM)

L'hypothèse de propagation du chaos nous a amenés à nous intéresser à la loi $P_N$, qui décrit à chaque instant la répartition des potentiels $u_i(t)$ sur l'aléa pour tout réseau de taille $N$. La mise en uvre des équations de champ moyen repose sur le résultat mathématique suivant : la loi $P_N$ tend vers une loi gaussienne $P$ à la limite thermodynamique. Cette convergence est de plus extrêmement rapide, si bien que pour des tailles de l'ordre de $N=100$, la répartition des potentiels obéit presque à une gaussienne. C'est d'ailleurs ce qui a pu être observé sur les figures 2.3 et 2.4.

La loi $P(t)$ (restriction de $P$ à l'instant $t$) donne à l'instant $t$ la répartition des potentiels. Du fait de son caractère gaussien, la loi $P(t)$ est entièrement décrite par sa moyenne $\mu(t)$ et sa variance $\nu(t)$. La loi $Q(t)$, qui porte sur les activations, a pour moyenne $m(t)$ et pour moment d'ordre 2 $q(t)$. Les équations de champ moyen donnent l'évolution de ces grandeurs au cours du temps. Elles fournissent donc une description dynamique de ces grandeurs statistiques ``macroscopiques''. Plus précisément, pour $t$ de 1 à $T$, on a les équations couplées :

$$\left\{ \begin{array}{c} \displaystyle{\mu(t)=\bar{J}m(t-1)-\bar{... ...aystyle{\nu(t)=\sigma_J^2q(t-1)+\sigma_\theta^2+\sigma_W^2} \end{array} \right.$$ (2.4)

où $\bar{\theta}$ est la moyenne des seuils, $\sigma _\theta$ l'écart-type des seuils et $\sigma_W$ l'écart-type du bruit. La moyenne des activations $m(t)=\int x_i(t) dQ(t)$ et le moment d'ordre 2 $q(t)=\int x_i(t)^2 dQ(t)$. La loi $Q(t)$ est la loi image de $P(t)$ par la fonction de transfert $f_g$, et l'expression explicite de $m(t)$ et $q(t)$ est :

$$\left\{ \begin{array}{c} \displaystyle{m(t)=\int f_g\left(h\... ...f_g^2\left(h\sqrt{\nu(t)}+\mu(t)\right) Dh} \end{array}\right.$$

où le terme $Dh$ désigne le terme d'intégration gaussien $Dh=1/\sqrt{2\pi}\exp(-h^2/2)dh$.

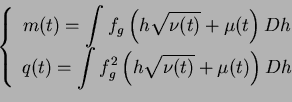
Ces équations ont été prouvées, pour $t$ de 0 à $T$, dans le cas où le bruit $W_i(t)$ est non nul [84]. Néanmoins, il n'y a aucune contrainte sur la valeur de ce bruit ; le terme de bruit $\sigma_W$ peut être pris aussi petit qu'on le souhaite. Toutes les expériences numériques qui ont été faites sur le cas non bruité semblent confirmer la validité des équations de champ moyen dans ce cadre.

Les équations de champ moyen fournissent donc un processus itératif permettant, à partir de la distribution initiale des potentiels, de déduire la distribution des potentiels (et des activations) à tout instant. Toute loi $P_N$ portant sur des réseaux de taille $N$ tend à tout instant à se comporter comme la loi limite $P$. La ressemblance entre la loi $P_N$ et la loi limite sera d'autant plus grande que la taille $N$ est élevée.

Les mesures sur la répartition $P_N$, effectuées dans le cas $N=100$, permettent de montrer l'excellente correspondance entre la loi $P_N(t_m)$ et la loi $P(t_m)$, avec $t_m=20$. On a représenté sur la figure 2.17 la répartition empirique provenant de simulations portant sur un nombre important de réseaux et la répartition théorique issue des équations de champ moyen. On constate une excellente concordance entre valeurs empiriques mesurées sur 10000 réseaux de taille $N=100$ ( $\langle\mu_N\rangle(t_m)=-0.1002$, $\langle\nu_N\rangle(t_m)=0.370$) et valeurs theoriques ( $\mu(t_m)=-0.1$, $\nu(t_m)=0.373$) pour les paramètres $\sigma _J=1$, $\bar{J}=0$, $\bar{\theta}=0.1$ et $\sigma _\theta =0.1$, $t_m=20$. La notation $\langle.\rangle$ désigne une moyenne effectuée sur l'aléa.

Figure 2.17: Distribution empirique et distribution théorique. L'histogramme donne la répartition empirique sur l'aléa des $u_i(t_m)$, sur la base de mesures effectuées sur $10000$ réseaux définis selon des paramètres identiques. La courbe pleine donne le tracé de la répartition théorique de ces mêmes potentiels selon les équations de champ moyen. Les autres paramètres sont $N=100$, $\bar{J}=0$, $\sigma _J=1$, $\bar{\theta}=0.1$, $\sigma _\theta =0.1$, $g=4$, $t_m=20$.

Ainsi, pour toute valeur de $t_m$, il est possible de trouver une valeur de $N$ telle que la loi $P_N(t_m)$ soit aussi proche qu'on le souhaite de la loi $P(t_m)$. Cette assertion ne garantit cependant pas que $P_N(t)$ restera ``conforme'' à $P(t)$ pour des valeurs de $t>t_m$. En effet, les équations de champ moyen sont démontrées sur un intervalle de temps fini $1..T$. Il peut a priori exister un temps $t>T$ au delà duquel les deux distributions se mettent à diverger. C'est là un problème délicat d'interversion des limites : le comportement pour les temps longs de la loi limite $P(t)$ n'est pas nécessairement représentatif de celui de la loi $P_N(t)$, $N$ étant pris aussi grand qu'on le souhaite. Il se trouve cependant que dans le cas étudié où les couplages $J_{ij}$ suivent tous la même loi centrée, les équations de champ moyen tendent à converger vers un point fixe ( $\mu^*,\nu^*$), et donc vers une loi limite asymptotique $P^*$, qui décrit convenablement la loi asymptotique $P_N^*$ des systèmes de taille finie. On verra plus loin (voir page ) qu'il existe des modèles où cette propriété n'est plus vérifiée.