




suivant: Comportement dynamique
monter: Équations d'évolution à taille
précédent: Description du système
Table des matières
Index
Comportement statistique à taille finie
Les mesures que nous présentons ici ont pour but d'illustrer le rôle du paramètre de gain  et du seuil
et du seuil
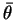 sur la répartition statistique des activations des neurones.
On ne s'intéresse (pour l'instant) pas au régime dynamique.
Nous présentons ici des répartitions empiriques fondées sur l'observation des activations et des potentiels sur les quelques pas de temps qui suivent l'initialisation.
sur la répartition statistique des activations des neurones.
On ne s'intéresse (pour l'instant) pas au régime dynamique.
Nous présentons ici des répartitions empiriques fondées sur l'observation des activations et des potentiels sur les quelques pas de temps qui suivent l'initialisation.
Les réseaux sont de taille 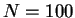 . Cette taille assure une bonne homogénéité des comportements dynamiques d'un réseau à l'autre.
Les paramètres invariants sont
. Cette taille assure une bonne homogénéité des comportements dynamiques d'un réseau à l'autre.
Les paramètres invariants sont 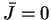 (poids synaptiques centrés),
(poids synaptiques centrés),
 et
et
 .
On regarde donc l'évolution des répartitions des potentiels
.
On regarde donc l'évolution des répartitions des potentiels  et des activations
et des activations 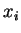 en modifiant les paramètres
en modifiant les paramètres  et
et
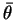 .
.
À 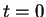 , les activations
, les activations 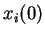 de chaque réseau sont initialisées suivant une loi uniforme en
de chaque réseau sont initialisées suivant une loi uniforme en ![$ ]0,1[$](img353.png) . On itère ensuite la dynamique jusqu'au temps
. On itère ensuite la dynamique jusqu'au temps 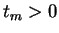 . On mesure alors le potentiel
. On mesure alors le potentiel  (ou l'activation
(ou l'activation  ) d'un seul neurone du réseau, d'indice
) d'un seul neurone du réseau, d'indice  .
Le temps
.
Le temps 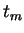 et l'indice
et l'indice  étant fixés, cette mesure de répartition porte sur l'aléa des réseaux, c'est à dire sur un grand nombre de tirages des poids qui définissent les systèmes.
Pour plusieurs jeux de paramètres
étant fixés, cette mesure de répartition porte sur l'aléa des réseaux, c'est à dire sur un grand nombre de tirages des poids qui définissent les systèmes.
Pour plusieurs jeux de paramètres  et
et
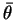 , on répète cette mesure sur
, on répète cette mesure sur 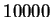 réseaux différents, ce qui permet d'obtenir des histogrammes de répartition assez précis.
réseaux différents, ce qui permet d'obtenir des histogrammes de répartition assez précis.
On constate en premier lieu que la convergence vers une répartition stationnaire est très rapide.
Sur la figure 2.2, on a representé trois répartition des potentiels obtenues pour les valeurs 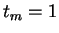 ,
, 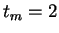 et
et 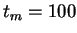 .
On voit alors clairement que dès le deuxième pas de temps, on est très près d'avoir atteint la répartition stationnaire.
En particulier, cette répartition stationnaire, qui correspond à une observation sur tous les réseaux de façon indifférenciée, est atteinte bien avant le régime stationnaire de la dynamique des réseaux individuels (voir page
.
On voit alors clairement que dès le deuxième pas de temps, on est très près d'avoir atteint la répartition stationnaire.
En particulier, cette répartition stationnaire, qui correspond à une observation sur tous les réseaux de façon indifférenciée, est atteinte bien avant le régime stationnaire de la dynamique des réseaux individuels (voir page ![[*]](/usr/share/latex2html/icons/crossref.png) ).
).
Figure 2.2:
Convergence vers la répartition stationnaire. On a représenté sur cette figure la répartition empirique sur l'aléa des  , pour (de gauche à droite)
, pour (de gauche à droite) 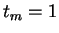 ,
, 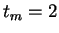 et
et 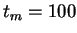 .
Les mesures ont été effectuées à chaque fois sur
.
Les mesures ont été effectuées à chaque fois sur 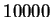 réseaux
différents.
Les histogramnmes font apparaître des répartitions centrées dont l'écart-type est de l'ordre de 0,7.
On constate que la convergence vers une répartition stationnaire est très rapide, puisqu'à
réseaux
différents.
Les histogramnmes font apparaître des répartitions centrées dont l'écart-type est de l'ordre de 0,7.
On constate que la convergence vers une répartition stationnaire est très rapide, puisqu'à 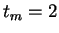 on a une répartition très proche de celle obtenue pour
on a une répartition très proche de celle obtenue pour 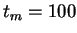 . Les autres paramètres sont
. Les autres paramètres sont 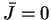 ,
,
 ,
,
 ,
,
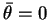 ,
,  .
.
|
|
Les mesures suivantes sont toutes effectuées au temps 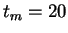 , temps auquel on s'attend à obtenir une répartition stationnaire.
, temps auquel on s'attend à obtenir une répartition stationnaire.
- Le premier jeu de figures (figure 2.3) a pour mission d'illustrer le rôle du paramètre de gain
 sur la répartition des activations
sur la répartition des activations 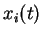 .
On voit que cette répartition des activations a une forme particulière en ``cuvette''.
Cette forme correspond au passage de la répartition gaussienne des
.
On voit que cette répartition des activations a une forme particulière en ``cuvette''.
Cette forme correspond au passage de la répartition gaussienne des 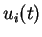 dans la fonction de transfert
dans la fonction de transfert 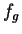 , qui répartit les valeurs non-linéairement sur l'intervalle
, qui répartit les valeurs non-linéairement sur l'intervalle ![$ ]0,1[$](img353.png) .
La loi des
.
La loi des 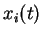 est plus précisément la loi image par la fonction de transfert de la loi des
est plus précisément la loi image par la fonction de transfert de la loi des 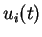 .
Ainsi, en changeant la valeur de
.
Ainsi, en changeant la valeur de  , on modifie la forme de la fonction de transfert ce qui a un effet direct sur la loi des
, on modifie la forme de la fonction de transfert ce qui a un effet direct sur la loi des 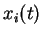 .
Sachant que l'augmentation du gain fait tendre la fonction de transfert vers une fonction seuil
.
Sachant que l'augmentation du gain fait tendre la fonction de transfert vers une fonction seuil
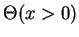 , la même augmentation de gain fait tendre la répartition des
, la même augmentation de gain fait tendre la répartition des 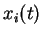 vers une répartition binaire.
Ainsi, la répartition en cuvette des activations tend à se creuser lorsque l'on augmente le gain.
Par contraste, on constate que la modification du paramètre
vers une répartition binaire.
Ainsi, la répartition en cuvette des activations tend à se creuser lorsque l'on augmente le gain.
Par contraste, on constate que la modification du paramètre  a peu d'influence sur la répartition des
a peu d'influence sur la répartition des 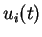 .
.
Le tableau 2.1 donne les valeurs de la moyenne égale à l'espérance sur l'aléa
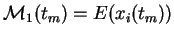 , du moment d'ordre 2
, du moment d'ordre 2
 , du moment d'ordre 3
, du moment d'ordre 3
 et du moment d'ordre 4
et du moment d'ordre 4
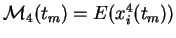 , à partir de la répartition des
, à partir de la répartition des  de la figure 2.3.
L'évolution de ces grandeurs empiriques est donnée en fonction de
de la figure 2.3.
L'évolution de ces grandeurs empiriques est donnée en fonction de  .
Les indicateurs appelés ``Gauchissement'' et ``Aplatissement'' donnent des indications sur le caractère non gaussien de la distribution (cette loi est par ailleurs calculable analytiquement, voir [9]) :
.
Les indicateurs appelés ``Gauchissement'' et ``Aplatissement'' donnent des indications sur le caractère non gaussien de la distribution (cette loi est par ailleurs calculable analytiquement, voir [9]) :
- Le Gauchissement (skewness) vaut
 , où
, où 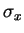 est l'écart-type
est l'écart-type
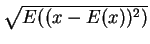 .
Il mesure le caractère asymétrique de la loi de part et d'autre de la valeur moyenne.
Pour une loi gaussienne, le gauchissement doit se rapprocher de zéro.
.
Il mesure le caractère asymétrique de la loi de part et d'autre de la valeur moyenne.
Pour une loi gaussienne, le gauchissement doit se rapprocher de zéro.
- L'Aplatissement (Kurtosis) vaut
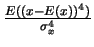 . Il donne une indication sur le caractère non-connexe de la distribution (plus l'aplatissement est proche de 1, plus la loi tend à présenter deux zones de forte densité disjointes).
L'Aplatissement d'une loi gaussienne vaut 3, celui d'une loi uniforme vaut 1.8, celui d'une loi binaire vaut 1.
. Il donne une indication sur le caractère non-connexe de la distribution (plus l'aplatissement est proche de 1, plus la loi tend à présenter deux zones de forte densité disjointes).
L'Aplatissement d'une loi gaussienne vaut 3, celui d'une loi uniforme vaut 1.8, celui d'une loi binaire vaut 1.
Tableau 2.1:
Valeur des moments de la répartition empirique sur l'aléa des  en fonction de
en fonction de  , sur une base de 10000 mesures, avec
, sur une base de 10000 mesures, avec 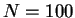 ,
, 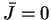 ,
,
 ,
,
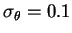 ,
,
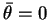 ,
, 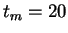 .
.
| g |
2 |
4 |
6 |
|
2 |
4 |
6 |
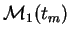 |
0.4960 |
0.5010 |
0.5029 |
|
|
|
|
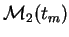 |
0.3626 |
0.4298 |
0.4563 |
Variance |
0.1166 |
0.1788 |
0.2033 |
 |
0.2965 |
0.3939 |
0.4327 |
Gauchissement |
0.0245 |
0.0245 |
-0.0143 |
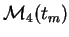 |
0.2550 |
0.3702 |
0.4170 |
Aplatissement |
1.5085 |
1.2221 |
1.1386 |
|
On constate à la lecture du tableau que l'aplatissement tend vers 1 lorsque  croît, ce qui illustre le fait que la distribution tend vers une distribution binaire pour g croissant.
On a donc un passage progressif de l'analogique au digital.
croît, ce qui illustre le fait que la distribution tend vers une distribution binaire pour g croissant.
On a donc un passage progressif de l'analogique au digital.
Figure 2.3:
Influence du gain sur la répartition des activations.
Les figures du haut donnent la répartition empirique sur l'aléa des  et les figures du bas donnent la répartition empirique sur l'aléa des
et les figures du bas donnent la répartition empirique sur l'aléa des  , toutes sur la base de
, toutes sur la base de 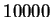 réseaux. On a de gauche à droite
réseaux. On a de gauche à droite 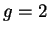 ,
,  et
et 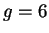 . On constate une influence forte du paramètre de gain sur la répartition des activations : une augmentation du gain tend à creuser la distribution et à rapprocher la distribution d'une distribution binaire. Les autres paramètres sont
. On constate une influence forte du paramètre de gain sur la répartition des activations : une augmentation du gain tend à creuser la distribution et à rapprocher la distribution d'une distribution binaire. Les autres paramètres sont 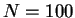 ,
, 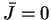 ,
,
 ,
,
 ,
,
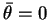 ,
, 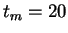 .
.
|
|
- Rappelons que les seuils
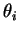 , tout comme les poids, sont fixés à l'initialisation du réseau selon une loi gaussienne
, tout comme les poids, sont fixés à l'initialisation du réseau selon une loi gaussienne
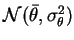 .
La deuxième série de figures 2.4, qui est à mettre en parallèle avec la précédente, montre, à
.
La deuxième série de figures 2.4, qui est à mettre en parallèle avec la précédente, montre, à  constant, l'influence du paramètre de moyenne sur les seuils
constant, l'influence du paramètre de moyenne sur les seuils
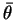 sur la répartition des activations
sur la répartition des activations 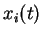 .
Plus précisément, une valeur positive de
.
Plus précisément, une valeur positive de
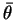 décale la répartition des potentiels
décale la répartition des potentiels 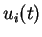 vers une gaussienne centrée en
vers une gaussienne centrée en
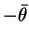 .
Cette non-symétrie se traduit sur la répartition des
.
Cette non-symétrie se traduit sur la répartition des 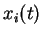 .
On voit donc que des seuils positifs tendent en moyenne à atténuer l'activation des neurones (et a contrario des seuils négatifs tendent à renforcer l'activation des neurones).
.
On voit donc que des seuils positifs tendent en moyenne à atténuer l'activation des neurones (et a contrario des seuils négatifs tendent à renforcer l'activation des neurones).
On donne dans le tableau 2.2 les valeurs de la moyenne
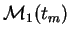 , du moment d'ordre 2
, du moment d'ordre 2
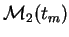 , du moment d'ordre 3
, du moment d'ordre 3
 et du moment d'ordre 4
et du moment d'ordre 4
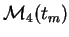 de la répartition des
de la répartition des  de la figure 2.4, en fonction de
de la figure 2.4, en fonction de
 .
On constate cette fois-ci que l'indicateur de gauchissement augmente avec
.
On constate cette fois-ci que l'indicateur de gauchissement augmente avec
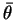 , ce qui illustre l'asymétrie croissante de la distribution.
, ce qui illustre l'asymétrie croissante de la distribution.
Tableau 2.2:
Valeur des moments de la répartition empirique sur l'aléa des  en fonction de
en fonction de
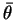 , sur une base de 10000 mesures, avec
, sur une base de 10000 mesures, avec
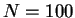 ,
, 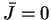 ,
,
 ,
,
 ,
,  ,
, 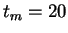 .
.
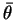 |
0 |
0.1 |
0.2 |
|
0 |
0.1 |
0.2 |
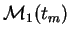 |
0.5010 |
0.4398 |
0.3645 |
|
|
|
|
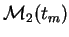 |
0.4298 |
0.3639 |
0.2829 |
Variance |
0.1788 |
0.1705 |
0.1500 |
 |
0.3939 |
0.3269 |
0.2452 |
Gauchissement |
0.0245 |
0.2397 |
0.5641 |
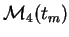 |
0.3702 |
0.3030 |
0.2218 |
Aplatissement |
1.2221 |
1.3070 |
1.6376 |
|
Figure:
Influence du seuil moyen
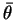 sur la répartition des activations.
Les figures du haut donnent la répartition empirique sur l'aléa des
sur la répartition des activations.
Les figures du haut donnent la répartition empirique sur l'aléa des  et les figures du bas donnent la répartition empirique sur l'aléa des
et les figures du bas donnent la répartition empirique sur l'aléa des  , toutes sur la base de
, toutes sur la base de 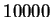 réseaux. On a de gauche à droite
réseaux. On a de gauche à droite
 ,
,
 et
et
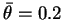 . La présence de seuils non centrés tend à décaler vers des valeurs négatives la répartition des
. La présence de seuils non centrés tend à décaler vers des valeurs négatives la répartition des  , ce qui se traduit par une asymétrie sur la distribution des
, ce qui se traduit par une asymétrie sur la distribution des  . Les autres paramètres sont
. Les autres paramètres sont 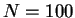 ,
, 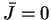 ,
,
 ,
,
 ,
,  ,
, 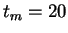 .
.
|
|
Ces premières mesures ont permis d'illustrer :
- l'homogénéité du comportements statistiques d'un grand ensemble de réseaux. Ce premier point permet de se familiariser avec les grandeurs manipulées dans le cadre des équations de champ moyen (voir page
![[*]](/usr/share/latex2html/icons/crossref.png) ).
).
- le caractère changeant de la répartition des
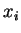 lorsque l'on fait varier les paramètres
lorsque l'on fait varier les paramètres  et
et 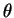 . La physionomie de la loi des activations a des effets importants sur le régime dynamique du réseau, et influence en particulier l'aspect du spectre de la jacobienne à la déstabilisation (voit page
. La physionomie de la loi des activations a des effets importants sur le régime dynamique du réseau, et influence en particulier l'aspect du spectre de la jacobienne à la déstabilisation (voit page ![[*]](/usr/share/latex2html/icons/crossref.png) ).
).





suivant: Comportement dynamique
monter: Équations d'évolution à taille
précédent: Description du système
Table des matières
Index
Dauce Emmanuel
2003-05-07
![]() et du seuil
et du seuil
![]() sur la répartition statistique des activations des neurones.
On ne s'intéresse (pour l'instant) pas au régime dynamique.
Nous présentons ici des répartitions empiriques fondées sur l'observation des activations et des potentiels sur les quelques pas de temps qui suivent l'initialisation.
sur la répartition statistique des activations des neurones.
On ne s'intéresse (pour l'instant) pas au régime dynamique.
Nous présentons ici des répartitions empiriques fondées sur l'observation des activations et des potentiels sur les quelques pas de temps qui suivent l'initialisation.
![]() . Cette taille assure une bonne homogénéité des comportements dynamiques d'un réseau à l'autre.
Les paramètres invariants sont
. Cette taille assure une bonne homogénéité des comportements dynamiques d'un réseau à l'autre.
Les paramètres invariants sont ![]() (poids synaptiques centrés),
(poids synaptiques centrés),
![]() et
et
![]() .
On regarde donc l'évolution des répartitions des potentiels
.
On regarde donc l'évolution des répartitions des potentiels ![]() et des activations
et des activations ![]() en modifiant les paramètres
en modifiant les paramètres ![]() et
et
![]() .
.
![]() , les activations
, les activations ![]() de chaque réseau sont initialisées suivant une loi uniforme en
de chaque réseau sont initialisées suivant une loi uniforme en ![]() . On itère ensuite la dynamique jusqu'au temps
. On itère ensuite la dynamique jusqu'au temps ![]() . On mesure alors le potentiel
. On mesure alors le potentiel ![]() (ou l'activation
(ou l'activation ![]() ) d'un seul neurone du réseau, d'indice
) d'un seul neurone du réseau, d'indice ![]() .
Le temps
.
Le temps ![]() et l'indice
et l'indice ![]() étant fixés, cette mesure de répartition porte sur l'aléa des réseaux, c'est à dire sur un grand nombre de tirages des poids qui définissent les systèmes.
Pour plusieurs jeux de paramètres
étant fixés, cette mesure de répartition porte sur l'aléa des réseaux, c'est à dire sur un grand nombre de tirages des poids qui définissent les systèmes.
Pour plusieurs jeux de paramètres ![]() et
et
![]() , on répète cette mesure sur
, on répète cette mesure sur ![]() réseaux différents, ce qui permet d'obtenir des histogrammes de répartition assez précis.
réseaux différents, ce qui permet d'obtenir des histogrammes de répartition assez précis.
![]() ,
, ![]() et
et ![]() .
On voit alors clairement que dès le deuxième pas de temps, on est très près d'avoir atteint la répartition stationnaire.
En particulier, cette répartition stationnaire, qui correspond à une observation sur tous les réseaux de façon indifférenciée, est atteinte bien avant le régime stationnaire de la dynamique des réseaux individuels (voir page
.
On voit alors clairement que dès le deuxième pas de temps, on est très près d'avoir atteint la répartition stationnaire.
En particulier, cette répartition stationnaire, qui correspond à une observation sur tous les réseaux de façon indifférenciée, est atteinte bien avant le régime stationnaire de la dynamique des réseaux individuels (voir page ![]() ).
).
![\includegraphics[]{hist_u_tm.eps}](img377.png)
![]() , temps auquel on s'attend à obtenir une répartition stationnaire.
, temps auquel on s'attend à obtenir une répartition stationnaire.
![]() , du moment d'ordre 2
, du moment d'ordre 2
![]() , du moment d'ordre 3
, du moment d'ordre 3
![]() et du moment d'ordre 4
et du moment d'ordre 4
![]() , à partir de la répartition des
, à partir de la répartition des ![]() de la figure 2.3.
L'évolution de ces grandeurs empiriques est donnée en fonction de
de la figure 2.3.
L'évolution de ces grandeurs empiriques est donnée en fonction de ![]() .
Les indicateurs appelés ``Gauchissement'' et ``Aplatissement'' donnent des indications sur le caractère non gaussien de la distribution (cette loi est par ailleurs calculable analytiquement, voir [9]) :
.
Les indicateurs appelés ``Gauchissement'' et ``Aplatissement'' donnent des indications sur le caractère non gaussien de la distribution (cette loi est par ailleurs calculable analytiquement, voir [9]) :
![]() croît, ce qui illustre le fait que la distribution tend vers une distribution binaire pour g croissant.
On a donc un passage progressif de l'analogique au digital.
croît, ce qui illustre le fait que la distribution tend vers une distribution binaire pour g croissant.
On a donc un passage progressif de l'analogique au digital.
![\includegraphics[]{hist_u_g2.eps}](img392.png)
![\includegraphics[]{hist_u_g4.eps}](img393.png)
![\includegraphics[]{hist_u_g6.eps}](img394.png)
![\includegraphics[]{hist_x_g2.eps}](img395.png)
![\includegraphics[]{hist_x_g4.eps}](img396.png)
![\includegraphics[]{hist_x_g6.eps}](img397.png)
![]() , du moment d'ordre 2
, du moment d'ordre 2
![]() , du moment d'ordre 3
, du moment d'ordre 3
![]() et du moment d'ordre 4
et du moment d'ordre 4
![]() de la répartition des
de la répartition des ![]() de la figure 2.4, en fonction de
de la figure 2.4, en fonction de
![]() .
On constate cette fois-ci que l'indicateur de gauchissement augmente avec
.
On constate cette fois-ci que l'indicateur de gauchissement augmente avec
![]() , ce qui illustre l'asymétrie croissante de la distribution.
, ce qui illustre l'asymétrie croissante de la distribution.
![\includegraphics[]{hist_u_theta0.eps}](img400.png)
![\includegraphics[]{hist_u_theta1.eps}](img401.png)
![\includegraphics[]{hist_u_theta2.eps}](img402.png)
![\includegraphics[]{hist_x_theta0.eps}](img403.png)
![\includegraphics[]{hist_x_theta1.eps}](img404.png)
![\includegraphics[]{hist_x_theta2.eps}](img405.png)