Description du système

On considère le système dynamique constitué par le jeu de $N$ équations couplées (2.1):

$$x_i(t)=f\left(\sum_{j=1}^N J_{ij} x_j(t-1) -\theta_i \right)$$ (2.1)

C'est, on le voit, un modèle à temps discret. Des intervalles de temps unitaires séparent la mise à jour des états. Ces intervalles peuvent être considéré comme des délais de transmission synaptique, réduits à leur expression la plus simple. La mise a jour étant effectuée en parallèle, on a à chaque mise à jour une multiplication de la matrice des poids $J=(J_{ij})_{i=1..N,j=1..N}$ par le vecteur d'états $x(t)=(x_1(t),...,x_N(t))^T$ auquel on soustrait le vecteur des seuils $\theta=(\theta_1,...,\theta_N)^T$. Le système admet donc comme écriture matricielle :

$$x(t)=f(Jx(t-1)-\theta)$$

La fonction de transfert $f$ est traditionnellement une fonction sigmoïdale, à valeurs sur ]-1,1[ ou ]0,1[. Une fonction de transfert à valeurs sur ]-1,1[ est en général considérée comme moins plausible biologiquement dans la mesure où le signe du produit $J_{ij}x_j(t-1)$ ne dépend pas uniquement du signe du lien synaptique, et ne permet pas de définir des liens excitateurs ou inhibiteurs. La plupart des études numériques porteront sur un système dont la fonction de transfert prend ses valeurs sur ]0,1[. Le choix de cette fonction de transfert n'est pas fondamental. On choisit de la faire dépendre du paramètre $g$, qui conditionne la forme de la fonction de transfert (voir figure 2.1) et en particulier la valeur de la dérivée en zéro. Cette valeur de la dérivée en zéro constitue le gain. Intuitivement, le gain donne une approximation du taux d'amplification d'un signal centré. La fonction de transfert qui sera utilisée par la suite est la fonction

$$f_g(x)=\frac{1+\tanh(gx)}{2}$$

de gain $g/2$. Plusieurs mesures exploratoires ont par ailleurs été effectuées sur les fonctions $g_g(x)=\frac{1+\mathrm{erf}(gx)}{2}$ et $h_g(x)=\frac{1}{2}+\frac{\arctan(\frac{\pi}{2} gx)}{\pi}$ sans modification qualitative du comportement dynamique : les valeurs de bifurcation changent, mais tous les modes dynamiques sont représentés. Enfin, il faut noter que lorsque $g$ tend vers l'infini, toutes ces fonctions tendent vers la fonction seuil $\Theta (x>0)$ qui provoque des sorties binaires. Dans la plage de valeurs que nous nous fixerons ($g$ prenant ses valeurs entre 2 et 20), les caractéristiques du signal de sortie resteront celles d'un signal continu.

Figure 2.1: influence du paramètre de gain $g$ sur la forme de la fonction de transfert $${f_g(x)=\frac{1+\tanh(gx)}{2}}$$. La fonction de transfert a été représentée pour des valeurs de $g$ égales (de gauche à droite) à 2, 4 et 6. On a représenté en pointillé la fonction seuil $\Theta (x>0)$.

Chacune des $N$ équations de (2.1) décrit la loi de mise à jour de l'état d'activation (ou l'activation) $x_i(t)$ de l'unité neuronale indexée par l'indice $i$. À chaque instant, l'activation du neurone au temps $t$ est conditionné par l'activation de tous les neurones à l'instant précédent.

On appelle dimension spatiale la dimension sur laquelle évolue l'indice $i$ et dimension temporelle la dimension sur laquelle évolue l'indice $t$. La moyenne spatiale désigne la moyenne sur tous les neurones à un instant donné, et la moyenne temporelle désigne la valeur moyenne d'un signal émis par un seul neurone. Notons au passage qu'il existe une autre dimension nécessaire pour les approches plus théoriques, appelée la dimension de l'aléa. Cette dimension porte sur l'ensemble des tirages aléatoires possibles selon les paramètres du modèle.

On distingue habituellement deux grandeurs qui permettent de décrire de façon plus détaillée les caractéristiques du neurone à l'instant $t$ :

• Champ local : c'est le terme de sommation des activations des autres neurones au temps $t-1$ pondéré par le poids synaptique $J_{ij}$. Ce terme représente l'influence à laquelle est soumis le neurone à cet instant.
  $$c_i(t)=\sum_{j=1}^N J_{ij}x_j(t-1)$$

• Potentiel de membrane (ou potentiel) : c'est le champ local auquel on soustrait le seuil, qui correspond à une influence propre conditionnant l'activation .
  $$u_i(t)=c_i(t)-\theta_i$$

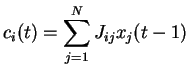
En fin de compte, on décrit habituellement le système par le jeu d'équations couplées (2.2).

$$\left\{ \begin{array}{l} \displaystyle{u_i(t)=\sum_{j=1}^N J_{ij} x_j(t-1) - \theta_i}\\ \displaystyle{x_i(t)=f(u_i(t))} \end{array} \right.$$ (2.2)

Du point de vue de l'interprétation biologique, on considère parfois que, dans le cas d'une fonction de transfert à valeurs sur $]0,1[$, l'activation $x_i(t)$ représente le taux de décharge du neurone sur l'intervalle $]t-1,t[$, la valeur 1 étant rapportée à la fréquence de décharge maximale. C'est l'interprétation traditionnelle des fonctions de transfert à états continus.

Une autre interprétation consiste à considérer la valeur de $x_i(t)$ comme une probabilité de décharge sur l'intervalle $]t-1,t[$. Cette interprétation peut être mise en uvre numériquement, auquel cas l'activation au temps $t$ dépend d'une probabilité et prend des valeurs binaires (un spike/pas de spike). À grande taille, ce modèle est équivalent à un modèle à états continus dont le champ local est bruité par un bruit gaussien ^2.1. Un tel modèle est présenté page .

L'approche que nous adopterons dans le cadre de cette thèse est sensiblement différente et sera justifiée plus loin. On établira un critère d'activité du neurone fondé sur l'écart-type du signal d'activation. Dans ce cadre, les neurones dont l'écart-type est faible sont considérés comme inactifs. Cela vaut pour les neurones dont le signal est saturé par la fonction de transfert.

La taille du réseau (nombre d'unités) est $N$. La matrice $J_{ij}$, de taille $N \times N$, décrit les couplages du réseau. L'espace des paramètres est de grande dimension, et, de ce fait, des prédictions sur le comportement asymptotique sont très difficiles. On a donc fixé certaines règles pour réduire l'espace des paramètres. Les poids sont des variables gaussiennes indépendantes et de moyenne $E(J_{ij})=\bar{J}/N$ et de variance var($J_{ij}$) =  $\sigma_J^2/N$, où $N$ est la taille du réseau et $\sigma_J$ l'écart-type de référence. On notera que la loi qui définit les tirages des poids synaptiques a été choisie de telle sorte que l'espérance et la variance de la somme des poids afférents $\sum_j J_{ij}$ ne dépendent pas de $N$, et valent respectivement $\bar{J}$ et $\sigma_J^2$. On impose de plus $J_{ii}=0$ (les neurones ne rebouclent pas sur eux-mêmes). Les seuils sont gaussiens, de moyenne $\bar{\theta}$ et de variance $\sigma_\theta^2$.

Les variables $g$, $\bar{J}$, $\sigma_J$, $\bar{\theta}$, $\sigma _\theta$ constituent les paramètres macroscopiques du système. Les valeurs précises des $J_{ij}$ et des $\theta_i$ issues d'un tirage aléatoire constituent les paramètres microscopiques du système.

Plusieurs remarques en découlent :

• Le tirage des poids et des seuils permet de caractériser entièrement le système dynamique. En introduisant cet aléa sur les poids, on se donne les moyens de construire autant de réseaux différents qu'on le souhaite. On parle de systèmes à aléa gelé pour caractériser des systèmes dépendant d'un tirage particulier.
• Pour obtenir une certaine homogénéité des comportements dynamiques d'un réseau à l'autre, on est amené à s'intéresser à des systèmes de grande taille. En effet, plus la taille est grande, plus les neurones tendront à se comporter statistiquement de la même manière, moins la dynamique dépendra du tirage initial des poids, et plus il sera facile de faire des prévisions sur le comportement de tels réseaux.
• Du fait de la loi qui définit les poids, les connexions sont (presque sûrement) asymétriques. Cette asymétrie des connexions synaptiques est une condition nécessaire pour obtenir des comportements dynamiques complexes. En brisant la contrainte de symétrie du modèle de Hopfield, on perd l'assurance de converger vers un point fixe.
• Toujours par opposition au modèle de Hopfield, le système possède pour une large plage de paramètres un bassin d'attraction unique ^2.2. Pour les paramètres courants que nous utiliserons, toute condition initiale mène donc au même attracteur. Dans ces conditions, l'apport d'information ne peut pas reposer sur la configuration des états initiaux, mais il faudra agir directement sur les paramètres microscopiques du système (valeurs des poids, valeurs des seuils).
• Le réseau est densément connecté, les connexions étant presque sûrement différentes de zéro. Il n'y a aucune géométrie au préalable dans un tel système, et en particulier chaque neurone est voisin de tous les autres neurones. À chaque instant, chaque neurone traite un signal de champ (champ local) qui se fonde sur la totalité de l'activité du réseau au temps précédent.