Distance entre deux trajectoires

Les équations de champ moyen décrivent une distribution théorique à chaque instant, mais ne fournissent pas d'indication sur les relations entre les états successifs atteints le long d'une trajectoire. Pour raisonner en termes de trajectoires, il faut partir d'un réseau référent, et décrire l'évolution des états au sein de ce réseau.

Si on considère un réseau de taille finie dont les poids et les seuils sont fixés une fois pour toutes, et que l'on tire indépendamment deux conditions initiales $u(0)$ et $u'(0)$, l'expression de la distance quadratique entre les deux trajectoires $u(t)$ et $u'(t)$ est donnée par

$$(d(t))^2=\frac{1}{N}\sum_{i=1}^N(u_i(t)-u_i'(t))^2$$

Par exemple, pour un réseau en régime de point fixe, quelle que soit la condition initiale, toute trajectoire individuelle $u(t)$ tend vers la valeur du point fixe $u^*$. Ainsi, si on considère deux conditions initiales différentes, et si on mesure à chaque instant la distance quadratique entre les deux trajectoires trajectoire, on constate qu'au cours du temps cette distance tend vers zéro.

Au contraire, pour un réseau en régime chaotique, les deux trajectoires tendent à s'éloigner au cours du temps jusqu'à approcher une valeur limite $d_{max}$ qui peut être considérée comme le diamètre de l'attracteur. Dans ce cas, pour deux conditions initiales aussi proches qu'on le souhaite, il existe un temps fini au bout duquel la distance entre les deux trajectoires atteindra l'ordre de grandeur de $d_{max}$.

On a représenté sur la figure 2.18 l'évolution de deux trajectoires individuelles $u_i(t)$ et $u_i'(t)$ sur un réseau de taille finie, pour le cas d'un régime de point fixe et le cas d'un régime chaotique. Dans le premier cas, on voit cette trajectoire tendre vers la même valeur limite pour les deux conditions initiales. Dans le second cas, on voit les deux trajectoires diverger au cours du temps, et présenter un comportement décorrélé au bout d'un temps fini.

Figure 2.18: Évolution de la distance entre trajectoires individuelles, en régime de point fixe et en régime chaotique. Les deux figures représentent l'évolution au cours du temps de deux trajectoires sur un même réseau. La première trajectoire (trait plein) $u_i(t)$ correspond à la condition initiale $u(0)$. La seconde trajectoire (trait pointillé) $u_i'(t)$ correspond à la condition initiale $u'(0)\neq u(0)$. La figure du haut correspond à un régime de point fixe ($g=4$), et la distance initiale $d(u(0),u'(0))=0,65$. La figure du bas correspond à un régime chaotique ($g=7$), et la distance initiale $d(u(0),u'(0))= 10^{-3}$. Paramètres : $N=100$, $\bar{J}=0$, $\sigma _J=1$, $\bar{\theta}=0.1$, $\sigma _\theta =0.1$, $i=1$.

La distance quadratique peut être décrite selon des paramètres macroscopiques à la limite thermodynamique [84]. Cette description nécessite de calculer la distance quadratique non plus sur l'ensemble des trajectoires individuelles d'un réseau donné, mais sur des trajectoires individuelles prises sur un grand nombre de réseaux. Cette méthode a été introduite par Derrida et Pommeau [86]. La loi de taille finie $P_N^2$ porte sur des trajectoires couplées $(u_i(t),u_i'(t))$ issues d'un même réseau et de deux conditions initiales différentes.

À la limite thermodynamique, on peut prouver que la loi $P_N^2$ tend vers la loi $P^2$, et l'expression de la distance quadratique est

$$(d(t))^2 = \int \int (u_i(t)-u_i'(t))^2 dP^2(t) = 2 (\nu(t)-\Delta(t))$$

où $\nu(t)$ est la variance des potentiels selon la loi $P(t)$ et $\Delta(t)$ est la covariance des potentiels :

$$\Delta(t)=\sigma_J^2C(t-1)+\sigma_\theta^2$$

et $C(t)$ est l'expression de la covariance sur les activations selon la loi $Q^2$, image de $P^2$ par la fonction de transfert.

$$C(t)=\int \int Dh Dh' f_g\left( h \frac {\sqrt{\nu(t)^2-\Delta(... ...a(t)} {\sqrt{\nu(t)}}+ \mu(t) \right) f_g\left( h' \sqrt{\nu(t)}+\mu(t) \right)$$

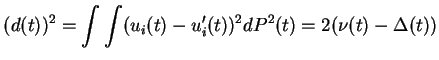
Ainsi, on peut décrire de manière explicite le comportement de la distance quadratique au cours du temps à la limite thermodynamique. Pour chaque jeu de paramètres ($\bar{J}$, $J$, $\bar{\theta}$, $\sigma _\theta$, $g$), on peut savoir si deux trajectoires tendent à se rapprocher ou au contraire à diverger sur le réseau générique.

On peut dès lors caractériser explicitement la dynamique pour les temps longs à la limite thermodynamique [80]. Soient $\mu^*$, $\nu^*$ et $\Delta^*$ les expressions de la moyenne, de la variance et de la covariance des potentiels pour les temps longs. On a alors :

• Si $\nu^*=\Delta^*$, la distance quadratique est nulle à la limite thermodynamique. La dynamique pour les temps longs est alors un point fixe tel que pour tout $t$, $u_i(t)=u_i^*$, où la valeur $u_i^*$ est issue d'un tirage selon la loi gaussienne ${\mathcal N}(\mu^*,{\nu^*}^2)$.
• Si $\nu^*>\Delta^*$, alors la distance entre 2 trajectoires pour $t$ grand a pour expression ${d^*}^2=E((u_i(t)-u_i'(t))^2)=2(\nu^*-\Delta^*)$. Cette valeur positive de la distance signifie que pour toute condition initiale, le signal $u_i(t)$ mesuré sur un réseau particulier suit pour les temps longs le processus gaussien $u_i(t)=u_i^*+b_i(t)$, où la valeur $u_i^*$ est issue d'un tirage selon la loi gaussienne ${\mathcal N}(\mu^*,{\nu^*}^2)$, et où $b_i(t)$ est un bruit blanc de variance $\nu^*-\Delta^*$.

Il apparaît donc que le système peut présenter à la limite thermodynamique deux régimes dynamiques différents : un régime de point fixe ( $\nu^*=\Delta^*$), et un régime de type processus gaussien ( $\nu^*>\Delta^*$), qui peut être interprété comme la description d'un régime chaotique à la limite thermodynamique. Pour $g$ croissant, la transition d'un régime à l'autre passe par une bifurcation, au cours de laquelle la valeur de $\nu^*$ ``dépasse'' celle de $\Delta^*$. On voit ainsi le caractère brutal de la transition du point fixe au chaos à la limite thermodynamique. Comme il a été conjecturé page , la plage de transition du point fixe au chaos se réduit à un point unique.

À la limite thermodynamique, il apparaît que le régime de chaos déterministe est décrit comme un processus aléatoire gaussien. Or, une dynamique de type stochastique peut être considéré comme ``plus désordonnée'' qu'une dynamique de type chaotique. À titre d'indication, le taux de divergence d'un processus stochastique discret est infini, c'est à dire qu'on n'a aucune mémoire des états antérieurs. À taille finie, la dynamique ne décrit jamais exactement un processus stochastique. Néanmoins, plus on s'éloigne de la frontière du chaos, plus la dynamique présente un aspect désorganisé. On peut alors parler de ``chaos profond'', et dans ce cas le processus gaussien décrit à la limite thermodynamique en est une excellente approximation.