




suivant: Synchronisation sur un modèle
monter: Équations de champ moyen
précédent: Distance entre deux trajectoires
Table des matières
Index
Variétés de bifurcation
Le calcul de la distance quadratique nous permet de décrire de façon explicite le régime dynamique générique pour un jeu de paramètres donné.
On peut donc décrire dans l'espace des paramètres macroscopiques ( ,
, 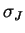 ,
,  ,
,
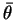 et
et
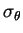 ) des frontières correspondant aux valeurs critiques de bifurcation entre un régime de point fixe et un régime chaotique.
On a représenté sur la figure 2.19 une telle variété de bifurcation, dans l'espace à 3 dimensions (
) des frontières correspondant aux valeurs critiques de bifurcation entre un régime de point fixe et un régime chaotique.
On a représenté sur la figure 2.19 une telle variété de bifurcation, dans l'espace à 3 dimensions ( ,
,
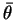 et
et
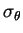 ).
).
Figure:
Variété de bifurcation. On a tracé sur cette figure la surface qui marque la séparation entre une dynamique de point fixe et une dynamique chaotique, à la limite thermodynamique, dans l'espace des paramètres
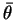 ,
,
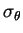 et
et  . On a fixé les paramètres
. On a fixé les paramètres 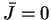 ,
,
 .
.
|
|
Une telle figure nous permet de tirer quelques conclusions sur les influences respectives des paramètres  ,
,
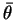 et
et
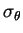 sur la dynamique des réseaux de taille finie.
sur la dynamique des réseaux de taille finie.
- L'augmentation du paramètre
 fait tendre la dynamique vers le chaos. À taille finie, l'augmentation de
fait tendre la dynamique vers le chaos. À taille finie, l'augmentation de  permet de mettre en évidence des routes vers le chaos par quasi-périodicité.
permet de mettre en évidence des routes vers le chaos par quasi-périodicité.
- La moyenne des seuils
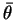 joue un rôle singulier.
On remarque une première tendance, qui indique que l'augmentation de
joue un rôle singulier.
On remarque une première tendance, qui indique que l'augmentation de
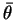 tend à favoriser le chaos.
Les lignes de bifurcation qui suivent les
tend à favoriser le chaos.
Les lignes de bifurcation qui suivent les
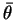 croissants sont en effet décroissantes.
Cependant, dans le cas où
croissants sont en effet décroissantes.
Cependant, dans le cas où
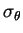 est faible, on trouve une valeur limite au delà de laquelle le chaos disparaît.
Un tel phénomène a été décrit dans [80], et est lié au fait que des seuils trop élevés, en tirant les potentiels vers des valeurs négatives, atteignent une valeur critique empêchant toute dynamique de se développer.
est faible, on trouve une valeur limite au delà de laquelle le chaos disparaît.
Un tel phénomène a été décrit dans [80], et est lié au fait que des seuils trop élevés, en tirant les potentiels vers des valeurs négatives, atteignent une valeur critique empêchant toute dynamique de se développer.
- Les lignes de bifurcation qui suivent les
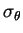 croissants sont croissantes. L'augmentation du paramètre
croissants sont croissantes. L'augmentation du paramètre
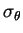 défavorise le développement de dynamiques chaotique, sauf dans le cas critique où
défavorise le développement de dynamiques chaotique, sauf dans le cas critique où
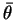 est élevé, auquel cas une augmentation de
est élevé, auquel cas une augmentation de
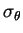 permet de produire une dynamique chaotique à condition que
permet de produire une dynamique chaotique à condition que  soit suffisamment élevé.
soit suffisamment élevé.
Ainsi, on voit que les méthodes issues de la physique statistique permettent de fixer les idées sur les comportements standards des réseaux aléatoires de grande taille.
Elles constituent un outil puissant pour une analyse et une compréhension approfondies de nos réseaux.





suivant: Synchronisation sur un modèle
monter: Équations de champ moyen
précédent: Distance entre deux trajectoires
Table des matières
Index
Dauce Emmanuel
2003-05-07
![]() ,
, ![]() ,
, ![]() ,
,
![]() et
et
![]() ) des frontières correspondant aux valeurs critiques de bifurcation entre un régime de point fixe et un régime chaotique.
On a représenté sur la figure 2.19 une telle variété de bifurcation, dans l'espace à 3 dimensions (
) des frontières correspondant aux valeurs critiques de bifurcation entre un régime de point fixe et un régime chaotique.
On a représenté sur la figure 2.19 une telle variété de bifurcation, dans l'espace à 3 dimensions (![]() ,
,
![]() et
et
![]() ).
).
![\includegraphics[]{carte_bif_3d.eps}](img548.png)
![]() ,
,
![]() et
et
![]() sur la dynamique des réseaux de taille finie.
sur la dynamique des réseaux de taille finie.