Régimes chaotiques sur le champ moyen

La section précédente met en avant des comportements oscillants sur les observables macroscopiques. Cependant, des dynamiques plus complexes, telles que des dynamiques chaotiques, peuvent également être observées sur le champ moyen, toujours dans le cadre d'un modèle mettant en jeu une population excitatrice et une population inhibitrice [91].

L'irruption d'un tel régime chaotique prend place sur un modèle légèrement différent de celui qui a été utilisé dans la section précédente. Ce modèle met toujours en uvre une population inhibitrice et une population excitatrice, mais la population inhibitrice possède cette fois-ci, au même titre que la population excitatrice, des liens récurrents propres. Ainsi, contrairement au précédent, ce modèle possède un schéma de connexion symétrique.

Les paramètres $d$ et $\sigma_J$ servent de nouveau à décrire la distance à zéro et l'écart-type de référence de la loi des poids. Un nouveau paramètre est introduit : le paramètre $a$ marque une nouvelle forme d'asymétrie sur la loi des poids : lorsque la valeur de $a$ est différente de 1, la loi des poids en provenance de la couche inhibitrice vers la couche excitatrice a un écart-type $\sigma _J^{(12)}$ différent de celui des autres lois, la moyenne restant la même. Autrement dit, l'inhibition moyenne reste la même, et l'influence de $a$ joue sur la dispersion autour de cette valeur moyenne.

$$\left\{ \begin{array}{ll} \bar{J}^{(11)}=\sigma_Jd & \sigma_J^{(1... ...ma_J\\ \bar{J}^{(22)}=-\sigma_Jd& \sigma_J^{(22)}=\sigma_J \end{array} \right.$$ (2.10)

Figure 2.28: Architecture du deuxième modèle à populations excitatrice et inhibitrice. Les poids ont des valeurs gaussiennes aléatoires. La population inhibitrice possède cette fois-ci des liens récurrents. L'écart-type $\sigma _J^{(12)}$ est réglé par le paramètre $a$.

Lorsque le paramètre $a$ vaut 1, donc, on constate de façon paradoxale que le modèle tend sur le champ moyen à se comporter exactement comme le modèle à une population. En particulier, la loi $P(t)$ tend vers un point fixe $P^*$ pour les temps longs, quelle que soit la valeur de la distance à zéro $d$. Même pour des valeurs de $d$ très élevées (c'est à dire pour des lois au caractère excitateur et inhibiteur très marqué), on n'observe pas d'oscillations synchronisées. Du fait de la symétrie du schéma de connexion, et de la symétrie des lois, l'influence excitatrice et l'influence inhibitrice se compensent exactement.

Une modulation du paramètre $a$ permet de briser de façon ``douce'' cette symétrie. C'est cette modulation qui permet de faire apparaître des comportements nouveaux sur le champ moyen. Pour obtenir ces comportements, il est par ailleurs nécessaire d'avoir un contraste fort entre la population excitatrice et la population inhibitrice, c'est à dire que $d$ ait une valeur supérieure à 15.

Pour les valeurs $d=30$, $a=0.5$, $\sigma _J=1$, il est possible de mettre en évidence une route vers le chaos sur le système macroscopique (2.6) pour des valeurs de $g$ croissantes. Une telle route vers le chaos est présentée figure 2.29. 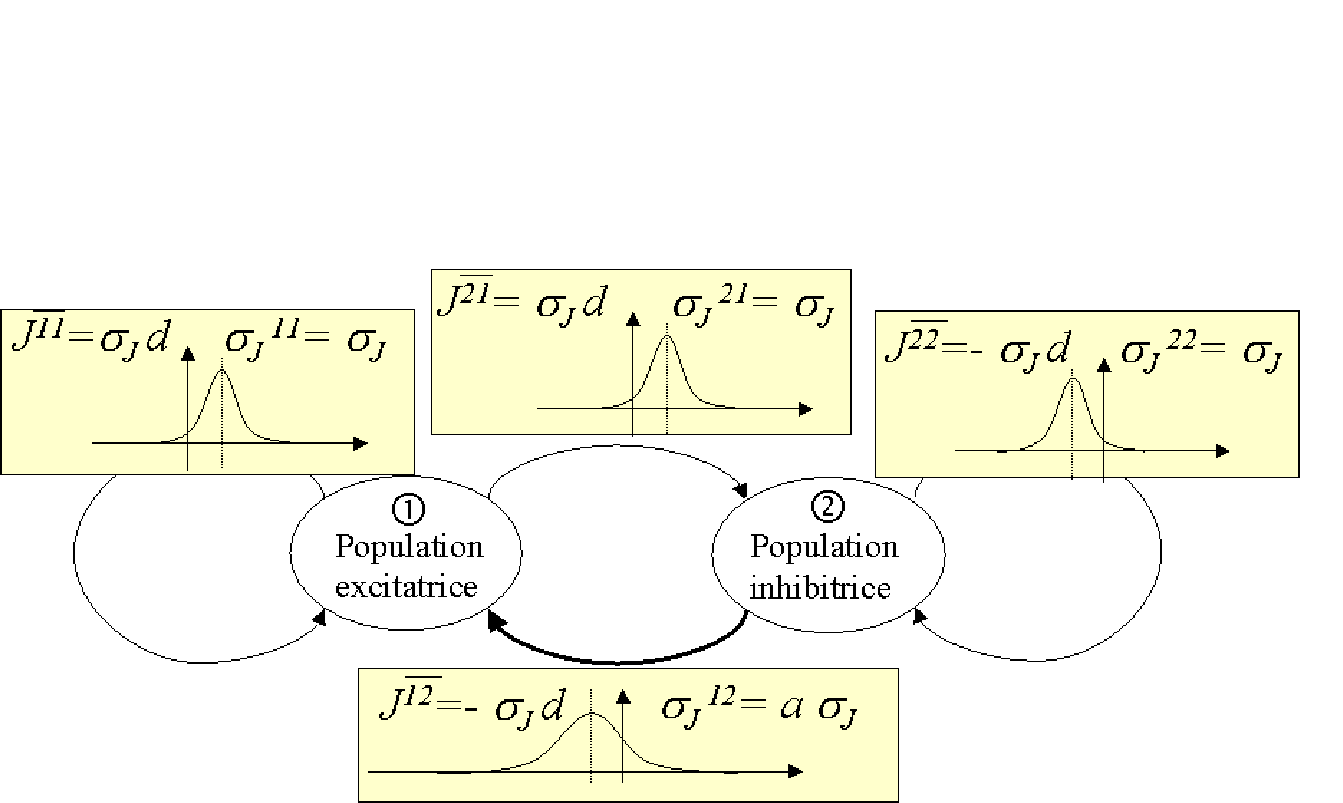Pour les paramètres choisis, cette route ne met pas en jeu de dynamiques toriques ni d'accrochage de fréquence  : le système passe directement du cycle au chaos aux alentours de $g=1.55$ (la figure présente l'attracteur chaotique atteint pour $g=2.5$, dans la mesure où la structure feuilletée de l'attracteur était peu visible pour des valeurs de $g$ inférieures).

Figure 2.29: Route vers le chaos par quasi-périodicité sur le signal de champ moyen. Représentation en 3 dimensions du signal $\mu ^{(1)}(t)$, pour un régime de point fixe ($g=1.3$, en haut à gauche), un régime cyclique ($g=1.4$, en haut à droite), un autre régime cyclique ($g=1.5$, en bas à gauche) et un régime chaotique ($g=2.5$, en bas à droite). La représentation est en 3D selon $(t-2,t-1,t)$. Paramètres : $a=0.5$, $d=30$, $\sigma _J=1$, $\bar{\theta}^{(1)}=0$, $\sigma _\theta ^{(1)}=0$, $\bar{\theta}^{(2)}=0$, $\sigma _\theta ^{(2)}=0$.

Pour les valeurs $d=30$, $a=2$, $\sigma _J=1$, la transition du point fixe au chaos s'opère de manière différente. Il s'agit dans ce cas d'une route vers le chaos par doublement de période. Lorsque $g$ croît, une première bifurcation fait apparaître un régime cyclique de période 2, suivi à la bifurcation suivante d'un régine de période 4, puis un peu plus loin d'un régime de période 8 etc... La distance entre deux bifurcations successives décroît, si bien que ces bifurcations de plus en plus rapprochées finissent par s'accumuler à l'approche d'une valeur critique $g_c$ proche de 0.9, qui marque l'entrée dans un régime chaotique. Il existe, pour des valeurs de $g$ supérieures, des fenêtres de périodicité. Cette route vers le chaos est également une route classique que l'on peut retrouver dans de nombreux systèmes. Sa présence dans le système du champ moyen marque son caractère générique. Cette route par doublement de période est présentée sur la figure 2.30.

Figure 2.30: Route vers le chaos par doublement de période sur le signal de champ moyen. 400 valeurs du signal $m^{(1)}(t)$ en dynamique stationnaire sont calculées pour différentes valeurs de $g$ (par pas de 0.01, en abcisse). Paramètres : $a=2$, $d=30$, $\sigma _J=1$, $\bar{\theta}^{(1)}=0$, $\sigma _\theta ^{(1)}=0$, $\bar{\theta}^{(2)}=0$, $\sigma _\theta ^{(2)}=0$.

Il est important d'insister sur la différence fondamentale entre les routes vers le chaos sur le système macroscopique et les routes vers le chaos que l'on peut observer sur les réseaux de taille finie à une population. Le comportement chaotique des grandeurs macroscopiques du champ moyen signifie que les observables macroscopiques des réseaux de taille finie, comme la moyenne, manifestent un comportement chaotique qui n'est pas réductible à une fluctuation aléatoire autour d'une valeur limite stationnaire. Sur ce régime, la dynamique est fortement non-stationnaire. Contrairement à la section précédente, il n'est pas possible de ramener cette non-stationnarité à une cyclo-stationnarité, dans la mesure où la moyenne suit une trajectoire chaotique de grande amplitude. Les neurones sont synchronisés sur un signal de nature chaotique, et l'on peut à ce titre parler de régime de chaos synchronisé.

Ce régime de chaos synchronisé peut être mis en évidence sur le modèle de taille finie. Contrairement aux régimes de taille finie reposant sur des oscillations synchrones, pour lesquels les signaux individuels tendent à atteindre leur valeur maximale de manière périodique, le régime de chaos synchronisé se caractérise par le fait que les signaux individuels tendent à atteindre leur maximum en même temps, mais cette fois-ci de façon apériodique. La figure 2.31 montre le comportement des signaux de potentiel $u_i^{(1)}(t)$ sur un réseau de taille finie en régime de chaos synchronisé. La similitude entre les différentes trajectoires est manifeste ; celles-ci présentent deux à deux une corrélation non nulle. Néanmoins, chacune prise individuellement produit un signal fortement apériodique.

Figure 2.31: Comportement chaotique synchronisé sur un réseau de taille finie. On peut noter la forte ressemblance avec des signaux d'EEG. 20 signaux $u_i^{(1)}(t)$ sont extraits du même réseau, en régime de chaos synchronisé, sur 200 pas de temps. Paramètres : $g=6$, $N=800$, $a=1.2$, $d=30$, $\sigma _J=1$, $\bar{\theta}^{(1)}=0$, $\sigma _\theta ^{(1)}=0$, $\bar{\theta}^{(2)}=0$, $\sigma _\theta ^{(2)}=0$.

Cette mise en évidence de régimes chaotiques sur le champ moyen illustre la difficulté à prouver la convergence des systèmes de taille finie vers le champ moyen pour les temps longs (voir page ) . En effet, dans la mesure où la loi $P^{(1)}(t)$, décrite par le champ moyen est chaotique, celle-ci devient extrêmement sensible aux petites variations sur la loi qui fixe les conditions initiales. Toute dynamique sur un réseau de taille finie est issue d'un tirage aléatoire des valeurs initiales des activations. Or, quelle que soit la taille $N$, ce tirage particulier s'éloigne légèrement du tirage ``idéal''. Il existe donc nécessairement un temps au delà duquel la trajectoire du signal moyen $m_N^{(1)}(t)$ sur ce réseau particulier et celle du signal de champ moyen $m^{(1)}(t)$ divergeront. Le caractère prédictif des équations de champ moyen ne peut être prouvé que sur un intervalle de temps fixé $1..T$, auquel cas il est possible de trouver une taille $N$ au delà de laquelle le système de taille finie et le champ moyen se comportent de la même façon sur l'intervalle $1..T$.