Champ moyen à la limite thermodynamique

Comme dans le modèle à une population, il est possible de prédire le comportement dynamique des observables macroscopiques $m^{(p)}(t)$ (espérance de l'activation $x_i^{(p)}(t)$), $q^{(p)}(t)$ (moment d'ordre 2 de l'activation), $\mu^{(p)}(t)$ (espérance du potentiel $u_i^{(p)}(t)$) et $\nu^{(p)}(t)$ (variance sur les potentiels) à la limite thermodynamique, c'est à dire de mettre en place des équations de champ moyen. Les méthodes mises en uvre pour aboutir à ces équations sont assez semblables à celles qui ont été utilisées pour le modèle à une population.

En particulier, la propagation du chaos reste vraie dans le modèle à deux populations. De même, tous les neurones d'une population $p$ donnée tendent à se comporter comme un neurone générique dont la loi du potentiel est $P^{(p)}$ et dont la loi de l'activation est $Q^{(p)}$. Les équations de champ moyen donnent l'évolution des lois $P^{(p)}(t)$ et $Q^{(p)}(t)$ au cours du temps.

On considère également :

$$m^{(p)}(t)=\int x_i^{(p)}(t) dQ^{(p)}$$

$$q^{(p)}(t)=\int (x_i^{(p)}(t))^2 dQ^{(p)}$$

et on note $Dh=\frac{1}{\sqrt{2\pi}}\exp(-h^{2}/2)dh$.

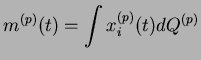
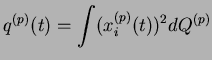
Les équations de champ moyen deviennent :

Pour $p\in \{1,2\}$ et $1\leq t\leq T-1~$ :

$$\left\{ \begin{array}{l} \mu^{(p)}(t+1)=-\bar{\theta}^{(p)}+\bar{... ...gma_J^{(p1)}}^{2}q^{(1)}(t)+{\sigma_J^{(p2)}}^{2}q^{(2)}(t) \end{array} \right.$$ (2.6)

avec

$$\left\{ \begin{array}{l} \displaystyle{m^{(p)}(t)=\int f_g(\... ...{2}(\sqrt{\nu ^{(p)}(t)}h+\mu ^{(p)}(t))Dh} \end{array}\right.$$

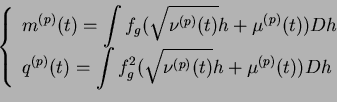
Ces équations permettent comme précédemment d'anticiper le comportement des grands systèmes de taille finie, cette fois-ci pour des systèmes à deux populations.