Équation d'évolution

Le modèle contient deux populations de neurones, dont le type est donné par $p$. Pour $p\in \{1,2\}$, il y a $N^{(p)}$ neurones dans la population $p$. $N=N^{(1)}+N^{(2)}$ est le nombre total de neurones. Pour $p,q\in \{1,2\}^2$, les $(J^{(pq)}_{ij})$ représentent les poids de la population $q$ vers la population $p$. Les $\theta_{i}^{(p)}$ sont les seuils et $W_{i}^{(p)}(t)$ est un bruit synaptique.

La dynamique devient : pour $p\in \{1,2\}$ et $1\leq i\leq N^{(p)}$,

$$\left\{ \begin{array}{l} \displaystyle{u_{i}^{(p)}(t)=\sum_{j=1}^... ...{(p)}}\\ \displaystyle{x_{i}^{(p)}(t)=f_g(u_{i}^{(p)}(t))} \end{array} \right.$$ (2.5)

$f_g$ est la fonction de transfert de $\mathbb{R}$ vers $]0,1[$, et vaut toujours $f_g(x)=\frac{1+\tanh(gx)}{2}$, de gain $g/2$. Le réseau est complètement connecté. Les distributions des poids synaptiques et des seuils suivent respectivement les lois gaussiennes ${\mathcal N}(\frac{\bar{J}^{(pq)}}{N^{(q)}},\frac{(\sigma_J^{(pq)})^{2}}{N^{(q)}})$ et ${\mathcal N}(\bar{\theta}^{(p)},(\sigma_\theta^{(p)})^{2})$. Les valeurs sont tirées une fois pour toutes à la création de chaque réseau (aléa gelé). 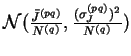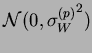Le bruit synaptique obéit également à une loi gaussienne ${\mathcal N}(0,{\sigma_W^{(p)}}^2)$, et ``nourrit'' la dynamique (le tirage est renouvelé à chaque pas de temps). Toutes ces variables aléatoires sont supposées indépendantes.

Le statut de ce bruit est un peu particulier sur notre modèle. En effet, dès l'instant où le système est bruité, il n'est plus possible de parler de chaos déterministe. Ce bruit est, comme dans le modèle à une population, nécessaire pour démontrer la propagation du chaos, et les équations de champ moyen qui en découlent. Néanmoins, une fois que ces équations sont établies, il est possible de mettre le terme de bruit $\sigma_W^{(p)}$ à zéro et de comparer le comportement du champ moyen à celui de modèles de taille finie déterministes.

Sur un modèle à deux populations, les paramètres macroscopiques qui définissent le système sont au nombre de 13 ( $\bar{J}^{(11)}$, $\sigma_J^{(11)}$, $\bar{J}^{(12)}$, $\sigma _J^{(12)}$, $\bar{J}^{(21)}$, $\sigma_J^{(21)}$, $\bar{J}^{(22)}$, $\sigma_J^{(22)}$, $\bar{\theta}^{(1)}$, $\sigma_\theta^{(1)}$, $\bar{\theta}^{(2)}$, $\sigma_\theta^{(2)}$, $g$).

Devant cette profusion, il s'avère nécessaire de définir un système macroscopique tel que les paramètres évoluent selon un nombre plus restreint de degrés de liberté. Les sections 2.3.2 et 2.3.3, qui définissent des populations excitatrices et inhibitrices, présentent deux exemples de telles restrictions.