Apprentissage d'un motif unique

La figure 4.9 montre l'évolution du signal moyen en cours d'apprentissage, pour une dynamique contrainte par un motif statique $I_1$. Le système passe progressivement d'une dynamique chaotique à une dynamique périodique.

Figure 4.9: Apprentissage en dynamique contrainte. À l'initialisation, la dynamique est contrainte par le motif $I_1$. Les 600 premiers pas de temps donnent la dynamique spontanée (chaotique). La règle d'apprentissage est itérée de $t=600$ à $t=1200$. L'apprentissage conduit à un régime périodique. La présentation d'un second motif $I_2$ non appris produit un nouveau régime chaotique. Une nouvelle présentation du motif initial produit un retour à la dynamique cyclique obtenue en fin d'apprentissage. Paramètres : $N=200$, $\alpha =0.1$, $\bar{I}=-0.4$, $\sigma _I=0.3$, $\bar{\theta=0}$, $\sigma _\theta =0$, $\bar{J}=0$, $\sigma _J=1$.

Pour le cas présenté, les effets de l'apprentissage sont circonscrits à la dynamique issue de la matrice des poids initiale et du motif $I_1$. En modifiant le motif d'entrée, on retrouve un comportement chaotique générique. Il suffit néanmoins de présenter à nouveau le motif $I_1$ pour reproduire à l'identique la dynamique atteinte en fin d'apprentissage. Le réseau a donc appris à associer un régime périodique spécifique à la stimulation $I_1$.

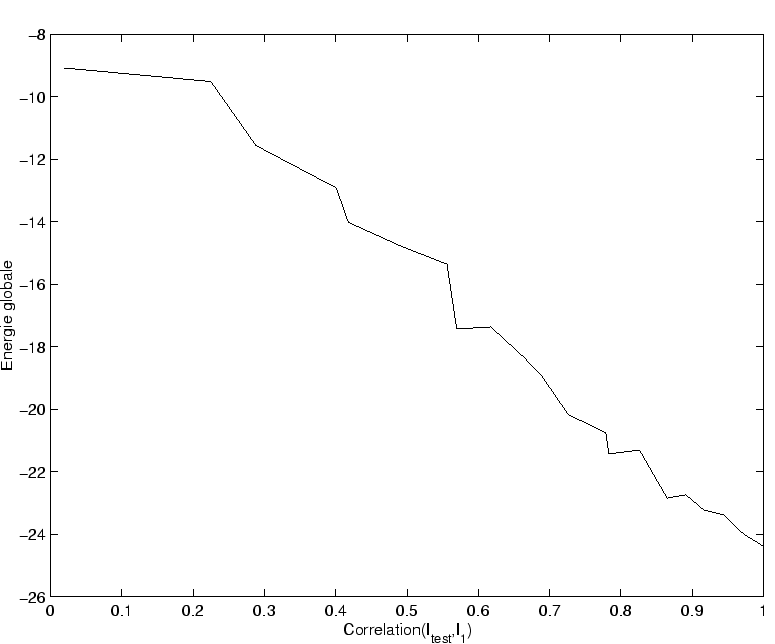
Plus généralement, la valeur de l'énergie globale $E$ attachée à la dynamique contrainte par le motif appris est nettement supérieure (en valeur absolue) à l'énergie globale attachée à un motif quelconque (voir figure 4.10). Rappelons que l'augmentation en valeur absolue de $E=\sum_i E_i=-\sum_{i,j}J_{ij}$cov$_{ij}^{[1]}$ correspond à une augmentation de l'amplitude des signaux d'activation, donc de l'activité dynamique. Tout motif ayant une corrélation positive avec $I_1$ tend à développer une activité dynamique plus importante que celle développée par un motif non corrélé. Les valeurs des termes d'énergie sont mesurées pour des motifs $I_{test}$ combinant les valeurs de $I_1$ et celles d'un autre motif tiré indépendamment $I_2$, comme $I_{test}=\bar{I}+\sqrt{1-\beta} (I_1-\bar{I})+\sqrt{\beta} (I_2-\bar{I})$, avec $\beta \in [0,1]$, tel que $E(I_{test})=\bar{I}$ et var$(I_{test})=\sigma_I^2$. La valeur $1-\beta$ donne l'espérance de la corrélation entre le motif $I_1$ et le motif $I_{test}$. On constate sur cette figure que l'intensité de l'activité dynamique est proportionnelle à la corrélation avec le motif appris. On a $E_{test}\simeq(1-\beta) E_1+\beta E_2$, où $E_1$ est l'énergie attachée au motif appris, $E_2$ l'énergie attachée en moyenne à un motif décorrélé $I_2$.

Figure 4.10: Comportement moyen du terme d'énergie globale selon la proximité avec le motif appris. La matrice des poids est issue d'un apprentissage sur 1200 pas de temps avec un motif de référence $I_1$. La valeur du terme d'énergie à l'issue de l'apprentissage vaut $-24,4$. L'abcisse donne la corrélation des motifs de test avec le motif $I_1$. Pour chaque valeur de la corrélation, on tire 20 motifs mixtes (combinaison entre $I_1$ et un motif aléatoire). Le terme d'énergie est moyenné sur les valeurs associées à ces 20 motifs. Paramètres : $N=200$, $\alpha =0.1$, $\bar{I}=-0.4$, $\sigma _I=0.3$, $\bar{\theta=0}$, $\sigma _\theta =0$, $\bar{J}=0$, $\sigma _J=1$.

Il apparaît donc que l'activité dynamique associée au motif $I_1$ tend à dominer en amplitude celle associée à tout autre motif. Le comportement initial du système, qui tendait à produire une activité du même ordre de grandeur pour tout motif, est révolu. La configuration associée à $I_1$ peut être qualifié de persistante, dans la mesure où cette configuration se maintient pour une famille de motifs présentant des caractéristiques communes avec $I_1$.

On appelle rayon d'action du motif $I_1$ la quantité $\beta_r=\frac{E_1}{E_1+E_2}$. Pour des motifs définis selon une valeur de $\beta<\beta_r$, le terme $E_1$ domine le terme $E_2$ sur la valeur de $E_{test}$, soit $(1-\beta)E_1>\beta E_2$. En ce sens, un apprentissage effectué sur des dynamiques de faible amplitude (cycles limites proches de la destabilisation), dont le terme d'énergie initial $E_2$ est faible, tendra à assurer au motif $I_1$ un rayon d'action élevé, et donc à faire baisser la spécificité de l'apprentissage. Il est ainsi préférable de pratiquer l'apprentissage sur des dynamiques nettement chaotiques, dont le terme d'énergie initial est élevé, afin de limiter le rayon d'action de l'apprentissage.