Motifs conditionnants

On cherche ici à fusionner information spatiale et information temporelle. Le motif statique peut être vu comme un motif conditionnant (drive). Dans la suite, ce motif est pris suffisamment ``fort'' pour imposer la configuration spatiale du réseau. Le motif dynamique vient se greffer sur cette configuration spatiale et impose la période de la dynamique. L'apprentissage sert ensuite à inscrire dans la dynamique les caractéristiques de la séquence. La présentation du motif conditionnant seul après apprentissage doit permettre de reproduire les caractéristiques spatiales et temporelles de la dynamique obtenue en fin d'apprentissage.

Le système contraint peut être réécrit comme :

$$\left\{ \begin{array}{l} u_i(t)=\sum_{j=1}^N J_{ij} x_j(t-1) - \theta_i + D_{i,m} + I_{i,m}(t)\\ x_i(t)=f_g(u_i(t)) \end{array} \right.$$ (4.5)

où $D_m$ est le motif conditionnant $m$, gaussien, de moyenne $\bar{D}$ et d'écart-type $\sigma _D$, et $I_m(t)$ le motif dynamique associé au motif conditionnant $m$, de moyenne $\bar{I}$, d'écart-type $\sigma _I$ et de période $\tau_m$.

Les résultats de simulations ci-dessous présentent un apprentissage effectué avec 5 motifs conditionnants $\{D_m\}_{m=1..5}$ et cinq motifs dynamiques $\{I_m(t)\}_{m=1..5}$ de périodes respectives $\tau_1=2$, $\tau_2=3$, $\tau_3=4$, $\tau_4=5$ et $\tau_5=6$ sur un réseau de taille $N=200$, avec $g=8$. Les motifs conditionnants et des motifs dynamiques associés sont toujours présentés simultanément. L'apprentissage est croisé, et le paramètre d'apprentissage est $\alpha =0.1$. Chaque séquence est présentée 60 fois, soit en tout 1200 pas d'apprentissage. On présente figure 4.12 le comportement dynamique du réseau après apprentissage, lorsque l'on présente une association ( $D_m, I_m(t)$), lorsque l'on présente $D_m$ seul, et lorsque l'on présente des motifs statiques conditionnants quelconques (motifs tests).

Figure 4.12: Signal d'activation moyen, après apprentissage, pour différentes stimulations. La figure du haut donne le signal moyen lorsque l'on stimule le réseau avec des couples ( $D_m, I_m(t)$). La figure du milieu donne le signal moyen lorsque l'on stimule le réseau avec les motifs conditionnants $D_m$ seuls. La figure du bas donne le signal moyen lorsque l'on stimule le réseau avec des motifs tests. Les motifs tests sont tirés selon $\bar{D}$, $\sigma _D$. Paramètres : $N=200$, $g=8$, $\alpha =0.1$, $\bar{D}=-0.4$, $\sigma _D=0.3$, $\bar{I}=0$, $\sigma _I=0.2$, $\bar{\theta}=0$, $\sigma _\theta =0$, $\bar{J}=0$, $\sigma _J=1$.

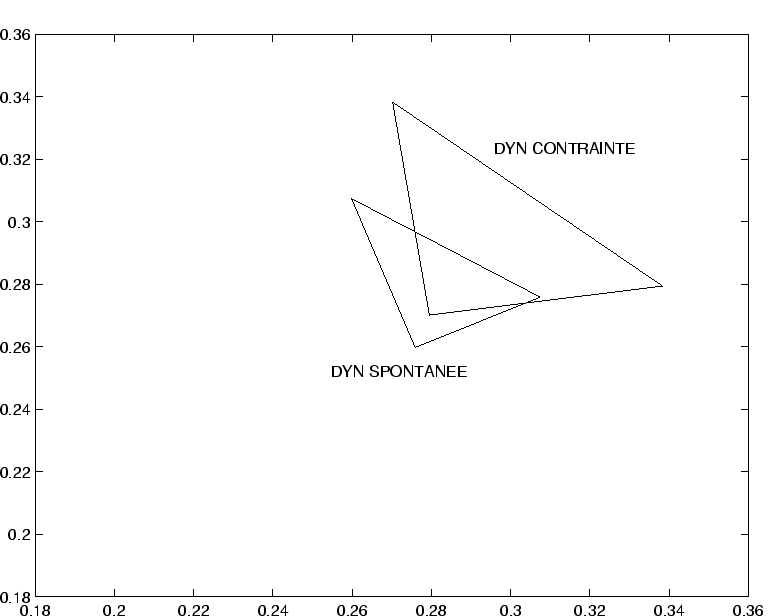
À l'issue de l'apprentissage, la dynamique contrainte par les couples ( $D_m, I_m(t)$), initialement chaotique, présente une périodicité stricte. La dynamique contrainte par les motifs conditionnants seuls reste chaotique, avec une périodicité marquée indiquant la proximité de la frontière du chaos. Les valeurs moyennes de cette dynamique se rapprochent des valeurs moyennes de la dynamique atteinte à la fin de l'apprentissage. La dynamique contrainte par des motifs tests reste, sur l'exemple présenté, fortement chaotique.

Le tableau 4.1 donne les valeurs de la période mesurée sur le signal moyen, pour différentes stimulations. La valeur de la période est fondée sur la mesure de la fréquence dominante apparaissant dans le spectre de Fourier. Avant apprentissage, les périodes trouvées en dynamique contrainte par les motifs conditionnants $D_m$ seuls sont décorrélées des périodes des motifs dynamiques $I_m(t)$ associés. Après apprentissage, la dynamique contrainte par les motifs conditionnants seuls reproduit la périodicité issue de la capture du signal $I_m(t)$ par le réseau. Des motifs quelconques définis selon les mêmes paramètres que les motifs conditionnants amènent une dynamique souvent chaotique dont la période est difficile à discerner. On a donc réussi à associer les motifs conditionnants à des régimes périodiques spécifiques.

Tableau: Période dominante mesurée sur le signal moyen, avant et après apprentissage, pour différentes stimulations. Les valeurs entre parenthèses indiquent que le signal est très chaotiques et que la valeur n'est pas fiable. Les motifs tests sont tirés selon $\bar{D}$, $\sigma _D$. Paramètres : $N=200$, $g=8$, $\alpha =0.1$, $\bar{D}=-0.4$, $\sigma _D=0.3$, $\bar{I}=0$, $\sigma _I=0.2$, $\bar{\theta}=0$, $\sigma _\theta =0$, $\bar{J}=0$, $\sigma _J=1$.

	$m=1$	$m=2$	$m=3$	$m=4$	$m=5$
	$(\tau_m=2)$	$(\tau_m=3)$	$(\tau_m=4)$	$(\tau_m=5)$	$(\tau_m=6)$
( $D_m, I_m(t)$) avant apprentissage	2	3	2	5	6
$D_m$ avant apprentissage	5.5	7.7	(8)	(40)	5
( $D_m, I_m(t)$) apres apprentissage	2	3	2	2.5	6
$D_m$ apres apprentissage	2	3	2	2.5	6
motifs tests apres apprentissage	(6.2)	6.9	3	(3)	(7.2)

Les termes d'énergie globale $E$ (voir tableau 4.2) permettent de mesurer l'évolution de l'activité dynamique associée aux différentes stimulations. Avant apprentissage, les systèmes stimulés périodiquement ont une activité dynamique d'amplitude deux fois plus importante, en moyenne, que celle des systèmes non stimulés périodiquement. À l'issue de l'apprentissage, le terme d'énergie associé aux couples ( $D_m, I_m(t)$) augmente comme prévu. Le terme d'énergie associé aux motifs conditionnants $D_m$ est en moyenne le double de celui associé à des motifs test. On constate néanmoins une forte augmentation de ce terme, même pour les dynamiques non-spécifiques. L'apprentissage provoque ici une augmentation globale de l'activité dynamique (qui est un peu plus que doublée pour les motifs non-spécifiques).

Tableau 4.2: Terme d'énergie globale $E$, avant et après apprentissage, pour différentes stimulations. Les motifs tests sont tirés selon $\bar{D}$, $\sigma _D$. Paramètres : $N=200$, $g=8$, $\alpha =0.1$, $\bar{D}=-0.4$, $\sigma _D=0.3$, $\bar{I}=0$, $\sigma _I=0.2$, $\bar{\theta}=0$, $\sigma _\theta =0$, $\bar{J}=0$, $\sigma _J=1$.

	$m=1$	$m=2$	$m=3$	$m=4$	$m=5$	moyenne
( $D_m, I_m(t)$) avant apprentissage	-5.6	-9.1	-9	-6.5	-6.9	-7.4
$D_m$ avant apprentissage	-1.5	-6.6	-6.6	-4.5	-2.9	-4.2
( $D_m, I_m(t)$) apres apprentissage	-23.9	-29.1	-30.6	-16	-29.2	-25.7
$D_m$ apres apprentissage	-18.9	-20.1	26.7	-9.9	-20.7	-19.3
motifs tests apres apprentissage	-8.8	-11.2	-12.3	-10.4	-10.2	-10.6

Enfin, pour calculer les données du tableau 4.3, on prend pour référence les 5 dynamiques associées aux couples $(D_m, I_m(t))_{m=1..5}$ après apprentissage. On cherche à voir dans quelle mesure les dynamiques associées aux motifs conditionnants $D_m$ imitent les dynamiques de référence. Après un test sur la phase, on calcule la corrélation entre chaque signal $x_i(t)$ et le signal d'activation de référence de même indice, et on fait la moyenne sur toutes ces corrélations. Il apparaît alors que pour $m$ fixé, seule la dynamique associée au motif $D_m$ présente une corrélation significativement élevée avec la dynamique de $(D_m, I_m(t))$. Les valeurs de corrélation obtenues pour les autres motifs appris sont tout aussi faibles que celles obtenues avec des motifs quelconques. La dynamique produite par $D_m$ possède donc des caractéristiques de celle produite par $(D_m, I_m(t))$, même si la corrélation est moins élevée que dans le cas de l'apprentissage d'une séquence unique.

On constate également que l'apprentissage est ``moins abouti'' pour certains motifs que pour d'autres. Le motif le mieux appris a une corrélation de 0.56 avec la dynamique de référence, et le moins bien appris une corrélation de 0.15. Bien que chaque séquence soit présentée le même nombre de fois au cours de l'apprentissage, il n'y a pas nécessairement homogénéité en terme de qualité d'apprentissage.

Tableau 4.3: Corrélation moyenne avec les signaux d'activation de référence (dynamique issue de ( $D_m, I_m(t)$)), après apprentissage, pour différentes les dynamiques issues des motifs conditionnants $D_m$ seuls, et les dynamiques issues de motifs tests. Les motifs tests sont tirés selon $\bar{D}$, $\sigma _D$. Paramètres : $N=200$, $g=8$, $\alpha =0.1$, $\bar{D}=-0.4$, $\sigma _D=0.3$, $\bar{I}=0$, $\sigma _I=0.2$, $\bar{\theta}=0$, $\sigma _\theta =0$, $\bar{J}=0$, $\sigma _J=1$.

	$m=1$	$m=2$	$m=3$	$m=4$	$m=5$	moyenne
$D_m$ apres apprentissage	0.49	0.56	0.38	0.15	0.44	0.4
motifs tests apres apprentissage	0.04	0.03	0.05	0.02	0.03	0.03

Ces données concernent un apprentisage effectué sur une réseau unique. Elles sont néanmoins représentatives de l'apprentissage effectué sur ce type de réseau. On constate en particulier, pour ces paramètres, qu'il existe une valeur limite du nombre de pas d'apprentissage au delà de laquelle la réponse du réseau se dégrade sérieusement, et le réseau perd la spécificité de ces réponses. Dans le cas présenté, cette valeur se situe aux alentours de 70 présentations, avec quelques variations d'un réseau à l'autre. Suivant la tâche que l'on se fixe, il semble y avoir une nombre de pas d'apprentissage optimal pour mener au mieux cette tâche. La qualité de la réponse obtenue pour ce nombre de pas optimal fixe en quelque sorte la capacité du réseau. Une mesure plus précise de la capacité des réseaux est proposée dans le chapitre suivant dans le cadre d'un modèle un peu plus élaboré.