 présentations (
présentations (
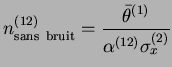 le nombre critique de présentations.
le nombre critique de présentations.
On constate en premier lieu qu'il y a statistiquement une durée d'apprentissage optimale, qu'on peut situer aux alentours de  présentations (
présentations (
![]() pas d'apprentissage), pour laquelle le taux de réussite est de l'ordre de 0.90, ce qui correspond au fait qu'une grand majorité de réseaux parvient à compléter correctement le signal partiel.
On appellera
pas d'apprentissage), pour laquelle le taux de réussite est de l'ordre de 0.90, ce qui correspond au fait qu'une grand majorité de réseaux parvient à compléter correctement le signal partiel.
On appellera
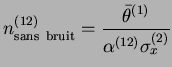 le nombre critique de présentations.
le nombre critique de présentations.
On sait que l'écart-type du signal retour, nul à l'initialisation parce que les poids sont nuls, augmente en cours d'apprentissage. Plus cet écart-type est élevé, plus le signal retour influence le potentiel des neurones de la couche primaire. Ainsi, au delà d'une certaine durée critique d'apprentissage, le signal retour est capable de produire une activation soutenue sur la couche primaire. C'est autour de cette valeur critique que s'opère le retournement de tendance observé. En effet :
Comme on l'a vu précédemment (page ![]() ),
),
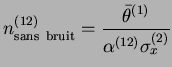 fournit une estimation du rapport signal sur bruit de l'activité de la couche dynamique.
On trouve une valeur de
fournit une estimation du rapport signal sur bruit de l'activité de la couche dynamique.
On trouve une valeur de
![]() , soit un rapport signal sur bruit à 0,44 .
L'amplitude du bruit est environ deux fois plus importante que celle du signal.
Autrement dit, lorsqu'un lien
, soit un rapport signal sur bruit à 0,44 .
L'amplitude du bruit est environ deux fois plus importante que celle du signal.
Autrement dit, lorsqu'un lien
![]() est renforcé par l'apprentissage, tout se passe comme si l'activité de la couche dynamique correspondait deux fois sur trois à des fluctuations aléatoires de l'activité de la couche dynamique et seulement une fois sur trois à une information pertinente.
L'apprentissage nécessite donc une certaine durée pour effectuer en quelque sorte un tri sur les signaux à extraire de l'activité de la couche dynamique.
est renforcé par l'apprentissage, tout se passe comme si l'activité de la couche dynamique correspondait deux fois sur trois à des fluctuations aléatoires de l'activité de la couche dynamique et seulement une fois sur trois à une information pertinente.
L'apprentissage nécessite donc une certaine durée pour effectuer en quelque sorte un tri sur les signaux à extraire de l'activité de la couche dynamique.
Le comportement du taux
![]() , relatif à un changement de motif conditionnant, est également intéressant.
Il donne des indications sur l'évolution du comportement réactif en cours d'apprentissage, qui traduit essentiellement l'effet de l'apprentissage sur les liens directs.
On constate que la qualité de la réponse réactive continue à augmenter assez longtemps après que le taux de réussite global se soit mis à chuter.
Cela traduit le mécanisme suivant : le changement de motif conditionnant statique produit une réorganisation dynamique qui change le circuit d'activation sur lequel s'appuie le signal retour. On remélange la donne en quelque sorte, si bien que les signaux retour non homogènes dans le cas où
, relatif à un changement de motif conditionnant, est également intéressant.
Il donne des indications sur l'évolution du comportement réactif en cours d'apprentissage, qui traduit essentiellement l'effet de l'apprentissage sur les liens directs.
On constate que la qualité de la réponse réactive continue à augmenter assez longtemps après que le taux de réussite global se soit mis à chuter.
Cela traduit le mécanisme suivant : le changement de motif conditionnant statique produit une réorganisation dynamique qui change le circuit d'activation sur lequel s'appuie le signal retour. On remélange la donne en quelque sorte, si bien que les signaux retour non homogènes dans le cas où
![]() , retrouvent leur homogénéité, qui leur permet de faire transiter la réponse réactive du réseau.
, retrouvent leur homogénéité, qui leur permet de faire transiter la réponse réactive du réseau.
On constate qu'il n'y a pas d'évolution sur la valeur de
![]() , qui correspond au taux de réussite d'un choix aléatoire parmi six réponses possibles (16% de réussite).
, qui correspond au taux de réussite d'un choix aléatoire parmi six réponses possibles (16% de réussite).