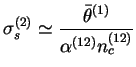L'apprentissage sur les liens retour permet ici d'illustrer le comportement réactif de la couche dynamique.
Les signaux présentés en entrée ne sont pas, pour ce paragraphe, des séquences, mais des inférences définies comme suit.
Une inférence est caractérisée par un couple ![]() , tel que dans le signal
, tel que dans le signal
![]() , si le neurone
, si le neurone ![]() est stimulé au temps
est stimulé au temps ![]() , le neurone
, le neurone ![]() est sytématiquement stimulé au temps
est sytématiquement stimulé au temps ![]() , avec
, avec
![]() et
et ![]() . Une base d'inférences de taille
. Une base d'inférences de taille ![]() est un ensemble
est un ensemble
![]() , tel que - 1 - tous les
, tel que - 1 - tous les ![]() sont différents et - 2 - la stimulation de
sont différents et - 2 - la stimulation de ![]() au temps
au temps ![]() est toujours suivi par celle du neurone
est toujours suivi par celle du neurone ![]() au temps
au temps ![]() , avec
, avec
![]() et
et
![]() .
.
On prend pour base d'apprentissage la base d'inférences
![]() , avec pour délai
, avec pour délai ![]() , afin de prendre en compte le délai de transmission à travers la couche dynamique.
Ainsi, si le neurone 1 est stimulé au temps
, afin de prendre en compte le délai de transmission à travers la couche dynamique.
Ainsi, si le neurone 1 est stimulé au temps ![]() , alors le neurone 2 est stimulé au temps
, alors le neurone 2 est stimulé au temps ![]() (même rapport entre la stimulation 3 et la stimulation 4).
Les couples sont répartis au hasard sur le signal temporel.
La probabilité d'apparition des deux couples est la même.
Des plages de silence sont maintenues entre les présentations de ces couples.
(même rapport entre la stimulation 3 et la stimulation 4).
Les couples sont répartis au hasard sur le signal temporel.
La probabilité d'apparition des deux couples est la même.
Des plages de silence sont maintenues entre les présentations de ces couples.
Le mécanisme est le suivant : Pour un couple (![]() ), la stimulation du neurone
), la stimulation du neurone ![]() sur la couche primaire envoie un signal sur la couche dynamique.
Cette stimulation est également appelée ``impulsion'' étant donné le caractère brutal de la transition par rapport au repos.
L'effet de cette impulsion est sensible au temps
sur la couche primaire envoie un signal sur la couche dynamique.
Cette stimulation est également appelée ``impulsion'' étant donné le caractère brutal de la transition par rapport au repos.
L'effet de cette impulsion est sensible au temps ![]() sur la couche dynamique.
La stimulation du neurone
sur la couche dynamique.
La stimulation du neurone ![]() de la couche primaire au temps
de la couche primaire au temps ![]() arrive en même temps que le signal retour qui prend en compte les effets de l'impulsion.
La règle d'apprentissage favorise alors les liens retour correspondant aux neurones chez qui l'impulsion initiale induit une variation significative d'activité.
Après apprentissage, la stimulation du neurone
arrive en même temps que le signal retour qui prend en compte les effets de l'impulsion.
La règle d'apprentissage favorise alors les liens retour correspondant aux neurones chez qui l'impulsion initiale induit une variation significative d'activité.
Après apprentissage, la stimulation du neurone ![]() tend à produire l'activation du neurone
tend à produire l'activation du neurone ![]() au temps
au temps ![]() via la couche dynamique.
via la couche dynamique.
Avec en entrée un signal conforme à la base ![]() , on itère la dynamique d'apprentissage sur 200 de pas de temps, avec
, on itère la dynamique d'apprentissage sur 200 de pas de temps, avec
![]() , en modifiant uniquement les poids retour.
Chaque couple est présenté 12 fois en tout.
, en modifiant uniquement les poids retour.
Chaque couple est présenté 12 fois en tout.
Pour tester l'effet de l'apprentissage, les neurones 1 ou 3 de la couche primaire sont stimulés isolément, et le signal évoqué sur la couche primaire via les poids retour est mesuré.
Il apparaît clairement sur la figure ![]() que pour le couple
que pour le couple ![]() , l'activation du neurone
, l'activation du neurone ![]() au temps
au temps ![]() se traduit par un pic d'activité du neurone
se traduit par un pic d'activité du neurone ![]() à
à ![]() , conformément à la base d'apprentissage.
, conformément à la base d'apprentissage.
|
|
Il faut noter que les impulsions envoyées sur la couche dynamique n'induisent pas de changement sensible sur le signal moyen
![]() parce que les liens directs sont centrés.
Le champ local des neurones de la couche dynamique est ponctuellement déplacé.
L'apprentissage sur les poids retour permet précisément de capter ces déplacements.
Les neurones 2 et 4 deviennent sensibles à une perturbation spécifique.
Sur la figure
parce que les liens directs sont centrés.
Le champ local des neurones de la couche dynamique est ponctuellement déplacé.
L'apprentissage sur les poids retour permet précisément de capter ces déplacements.
Les neurones 2 et 4 deviennent sensibles à une perturbation spécifique.
Sur la figure ![]() , on voit que si on prolonge la stimulation sur le neurone 1 de la couche primaire, le niveau d'activation du neurone 2 est nettement augmenté sur la même durée.
On voit donc bien que le neurone 2 réagit à la nouvelle configuration spatiale des activations induite sur la couche dynamique, c'est à dire à des différences de niveaux d'activité.
, on voit que si on prolonge la stimulation sur le neurone 1 de la couche primaire, le niveau d'activation du neurone 2 est nettement augmenté sur la même durée.
On voit donc bien que le neurone 2 réagit à la nouvelle configuration spatiale des activations induite sur la couche dynamique, c'est à dire à des différences de niveaux d'activité.
![\includegraphics[]{app_retour_plateau.eps}](img1112.png) |
Dernière remarque : vue la valeur d'
![]() choisie et le nombre de présentations, le niveau d'activation des neurones 2 et 4 demeure faible.
Ceci n'empêche pas l'interprétation et l'exploitation du comportement issu de l'apprentissage.
choisie et le nombre de présentations, le niveau d'activation des neurones 2 et 4 demeure faible.
Ceci n'empêche pas l'interprétation et l'exploitation du comportement issu de l'apprentissage.
On peut tenir sensiblement le même raisonnement que précédemment pour déterminer le nombre critique de présentations au delà duquel les neurones de la couche primaire deviennent sensibles au signal retour, au point d'atteindre des valeurs d'activation d'un ordre de grandeur comparable aux stimulations. Dans le cas où le signal d'entrée est une séquence, le franchissement de cette valeur permet l'entretien d'une chaîne d'activation (le signal retour tend alors à se substituer à la stimulation).
Dans le cas général, on peut estimer le nombre critique de présentations par le raisonnement suivant.
L'activation du neurone ![]() sur la couche primaire produit au cours de l'apprentissage un changement sur tous les liens
sur la couche primaire produit au cours de l'apprentissage un changement sur tous les liens
![]() , pour
, pour ![]() de 1 à
de 1 à ![]() .
L'intensité de ce changement vaut localement
.
L'intensité de ce changement vaut localement
![]() , et le changement total relatif aux
, et le changement total relatif aux ![]() afférents du neurone
afférents du neurone ![]() est de l'ordre de
est de l'ordre de
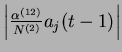 , où
, où
![]() est l'écart-type moyen des signaux d'activation de la couche dynamique, qui est de l'ordre de 0,25 pour
est l'écart-type moyen des signaux d'activation de la couche dynamique, qui est de l'ordre de 0,25 pour ![]() .
Si l'activation du neurone
.
Si l'activation du neurone ![]() était toujours précédée des mêmes valeurs d'activation sur la couche dynamique, le nombre de présentations critique serait de l'ordre de
était toujours précédée des mêmes valeurs d'activation sur la couche dynamique, le nombre de présentations critique serait de l'ordre de
Si maintenant, on suppose que l'on sait estimer par simulation le nombre critique
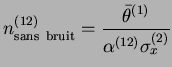 , il devient possible d'estimer à partir de ce nombre l'écart-type
, il devient possible d'estimer à partir de ce nombre l'écart-type
![]() correspondant à la partie significative (porteuse d'information) de l'activité de la couche dynamique comme
correspondant à la partie significative (porteuse d'information) de l'activité de la couche dynamique comme