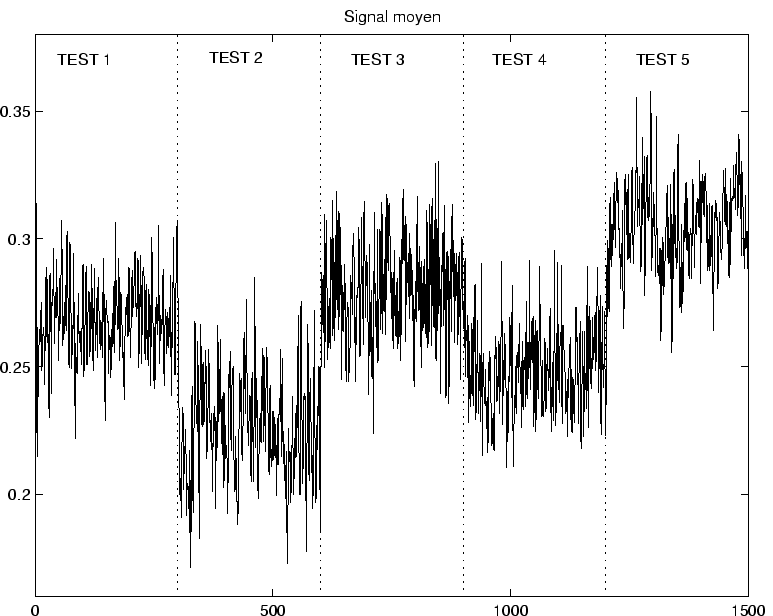
 et d'écart-type
et d'écart-type
 que l'on projette sur la couche primaire lorsque le motif
que l'on projette sur la couche primaire lorsque le motif Comme on l'a vu au chapitre 4, la couche dynamique est capable, après apprentissage, de produire un signal spécifique lorsqu'on la stimule avec l'entrée statique associée au cours du processus d'apprentissage. Cette propriété permet d'inscrire sur un même réseau plusieurs organisations dynamiques différentes, qui peuvent être activées à la commande.
Cette propriété peut bien sûr être exploitée sur le nouveau modèle.
À chaque motif conditionnant ![]() (gaussien, de moyenne
(gaussien, de moyenne
 et d'écart-type
et d'écart-type
![]() ) on associe pour les besoins de l'apprentissage une séquence
) on associe pour les besoins de l'apprentissage une séquence
 que l'on projette sur la couche primaire lorsque le motif
que l'on projette sur la couche primaire lorsque le motif ![]() est présent.
est présent.
Pendant l'apprentissage, les associations
![]() sont présentées les unes à la suite des autres, en laissant à chaque fois une soixantaine de transitoires, et en itérant la dynamique d'apprentissage sur une durée
sont présentées les unes à la suite des autres, en laissant à chaque fois une soixantaine de transitoires, et en itérant la dynamique d'apprentissage sur une durée ![]() .
Ce passage en revue de toutes les séquences compte comme une présentation, et correspond en tout à
.
Ce passage en revue de toutes les séquences compte comme une présentation, et correspond en tout à
![]() pas d'apprentissage.
La valeur de
pas d'apprentissage.
La valeur de ![]() donne le nombre de présentations.
donne le nombre de présentations.
Pour l'exemple présenté, toutes les séquences apprises sont de période 6, et non ambiguës.
De plus, les différentes séquences ne possèdent aucun neurone commun.
Il y a en tout 10 séquences qui activent les neurones numérotés de ![]() à
à ![]() .
On a calé la taille de la couche primaire sur les caractéristiques des stimulations, soit
.
On a calé la taille de la couche primaire sur les caractéristiques des stimulations, soit
![]() , autrement dit tous les neurones de cette couche appartiennent à l'une ou l'autre des séquences.
On autorise l'apprentissage sur tous les liens.
, autrement dit tous les neurones de cette couche appartiennent à l'une ou l'autre des séquences.
On autorise l'apprentissage sur tous les liens.
À l'issue de l'apprentissage, on calcule les taux de réussite en présentant successivement 10 séquences incomplètes qui stimulent un neurone sur 3, soit
![]() , avec le motif
, avec le motif ![]() associé sur la couche dynamique.
Le taux
associé sur la couche dynamique.
Le taux
![]() donne alors le rapport entre le nombre de réponses correctes et le nombre total de réponses testées.
On compare ce taux avec le taux
donne alors le rapport entre le nombre de réponses correctes et le nombre total de réponses testées.
On compare ce taux avec le taux
![]() que l'on obtient en stimulant le réseau avec
que l'on obtient en stimulant le réseau avec ![]() et en mettant un mauvais motif conditionnant, appartenant cependant à l'ensemble utilisé.
Le taux
et en mettant un mauvais motif conditionnant, appartenant cependant à l'ensemble utilisé.
Le taux
![]() correspond comme précédemment au taux de réussite obtenu lorsque l'on réinitialise les poids afférents à la couche dynamique.
correspond comme précédemment au taux de réussite obtenu lorsque l'on réinitialise les poids afférents à la couche dynamique.
La figure ![]() donne l'évolution de
donne l'évolution de
![]() ,
,
![]() et
et
![]() en fonction du nombre de présentations des séquences pendant l'apprentissage.
La moyenne a été effectuée sur 10 réseaux pour chaque valeur de
en fonction du nombre de présentations des séquences pendant l'apprentissage.
La moyenne a été effectuée sur 10 réseaux pour chaque valeur de ![]() , au lieu de 50 dans le cas précédent, pour des raisons de temps de calcul (4 nuits sur Sparc 10).
Ceci qui explique l'aspect plus accidenté de la courbe.
, au lieu de 50 dans le cas précédent, pour des raisons de temps de calcul (4 nuits sur Sparc 10).
Ceci qui explique l'aspect plus accidenté de la courbe.
|
|
La courbe présente les mêmes caractéristiques que précédemment : on constate qu'il y a un nombre de présentations optimal au delà duquel la qualité de la réponse du réseau chute rapidement.
Ce nombre optimal
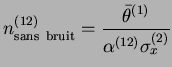 est légèrement inférieur au nombre obtenu précédemment, de l'ordre de 30 à 40 itérations.
Le taux de réussite maximal atteint est de l'ordre de 88%,
et le taux moyen pour
est légèrement inférieur au nombre obtenu précédemment, de l'ordre de 30 à 40 itérations.
Le taux de réussite maximal atteint est de l'ordre de 88%,
et le taux moyen pour ![]() entre 30 et 40 est de l'ordre de 80%.
On peut penser, comme cela se confirme sur des exemples individuels d'apprentissage, que sur 10 motifs présentés, environ 8 sont bien reproduits.
entre 30 et 40 est de l'ordre de 80%.
On peut penser, comme cela se confirme sur des exemples individuels d'apprentissage, que sur 10 motifs présentés, environ 8 sont bien reproduits.
On remarque que la chute du taux de réussite, lorsque
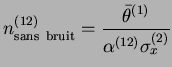 , est dépassé est beaucoup plus ``catastrophique'' que sur les exemples précédents.
Ce point illustre une sensibilité beaucoup plus prononcée à l'effet des activations parasites sur le signal retour.
En effet, le test sur la réponse du réseau évalue le maximum sur les 60 signaux d'activation.
Il suffit qu'un seul parmi les 60 neurones présente une activation parasite pour tout fausser.
Dès lors que les poids retour atteignent des valeurs critiques, l'hétérogénéité sur les 60 sorties tend rapidement à faire chuter le taux de réussite.
, est dépassé est beaucoup plus ``catastrophique'' que sur les exemples précédents.
Ce point illustre une sensibilité beaucoup plus prononcée à l'effet des activations parasites sur le signal retour.
En effet, le test sur la réponse du réseau évalue le maximum sur les 60 signaux d'activation.
Il suffit qu'un seul parmi les 60 neurones présente une activation parasite pour tout fausser.
Dès lors que les poids retour atteignent des valeurs critiques, l'hétérogénéité sur les 60 sorties tend rapidement à faire chuter le taux de réussite.
Le comportement du taux
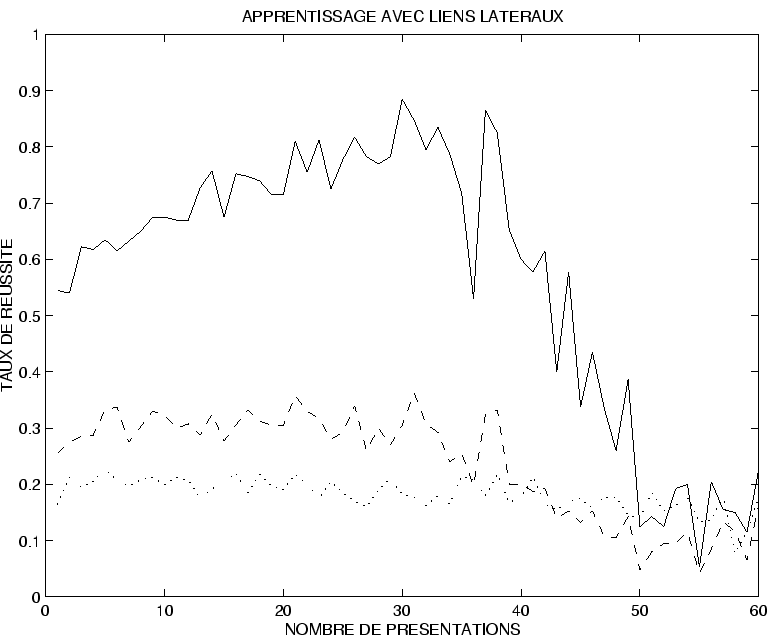
![]() , qui plafonne à 30% jusqu'à
, qui plafonne à 30% jusqu'à
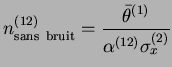 ,
montre que la présentation du mauvais motif conditionnant ne permet pas d'obtenir la bonne réponse.
On voit donc que l'évocation de la séquence apprise est bien dépendante de la présence du motif statique asssocié pendant l'apprentissage.
Seule la présence de ce motif permet de reconstituer la séquence apprise.
,
montre que la présentation du mauvais motif conditionnant ne permet pas d'obtenir la bonne réponse.
On voit donc que l'évocation de la séquence apprise est bien dépendante de la présence du motif statique asssocié pendant l'apprentissage.
Seule la présence de ce motif permet de reconstituer la séquence apprise.
Le même système possède donc différents modes de fonctionnement dépendant des motifs conditionnants. À chaque motif conditionnant correspond une séquence de sortie privilégiée, que l'on peut activer ou désactiver à volonté. La couche dynamique tient bien le rôle de ``réservoir à dynamiques''.
On a représenté sur la figure ![]() le comportement dynamique d'un réseau après un apprentissage où chaque association
le comportement dynamique d'un réseau après un apprentissage où chaque association
 est présentée 40 fois au cours de l'apprentissage.
Par ailleurs, les séquences ont une longueur variable, dont la période varie entre
est présentée 40 fois au cours de l'apprentissage.
Par ailleurs, les séquences ont une longueur variable, dont la période varie entre ![]() et
et ![]() .
.
On a plus précisément
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() et
et
![]() .
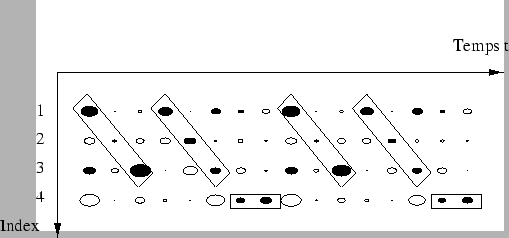
Après apprentissage, on présente successivement les
.
Après apprentissage, on présente successivement les  motifs
motifs ![]() sur une durée de l'ordre de 100 pas de temps, et on regarde le signal d'activation des 40 premiers neurones de la couche primaire.
Ces signaux d'activation sont représentés figure
sur une durée de l'ordre de 100 pas de temps, et on regarde le signal d'activation des 40 premiers neurones de la couche primaire.
Ces signaux d'activation sont représentés figure ![]() .
.
|
|
Après apprentissage, la présentation du motif ![]() tend à produire l'activation de la séquence associée sur la couche primaire (pour
tend à produire l'activation de la séquence associée sur la couche primaire (pour ![]() , on a donc dans ce cas légèrement dépassé la valeur critique).
On voit qu'environ 7 séquences sur 10 sont nettement reproduites sur la couche primaire.
On voit également qu'il existe quelques neurones parasites qui tendent à s'activer pour le mauvais motif conditionnant, et forment une sorte de bruit de fond sur le signal retour.
Pour les motifs conditionnants 1, 6 et 8, l'activité de fond sur la couche primaire est essentiellement chaotique, et aucune séquence ne se dégage sur le signal retour.
, on a donc dans ce cas légèrement dépassé la valeur critique).
On voit qu'environ 7 séquences sur 10 sont nettement reproduites sur la couche primaire.
On voit également qu'il existe quelques neurones parasites qui tendent à s'activer pour le mauvais motif conditionnant, et forment une sorte de bruit de fond sur le signal retour.
Pour les motifs conditionnants 1, 6 et 8, l'activité de fond sur la couche primaire est essentiellement chaotique, et aucune séquence ne se dégage sur le signal retour.
Il faut noter que l'activité qui se développe sur la couche primaire est entièrement pilotée par la couche dynamique, puisqu'aucun signal n'est projeté sur la couche primaire. La seule information provient des motifs conditionnants, et porte sur la configuration spatiale des activations, qui sert donc de guide pour la mise en place du bon circuit d'activation.