Déstabilisation

Dans les modèles à deux populations, l'étude de la divergence des trajectoires individuelles repose sur les mêmes principes que dans le modèle à une population. La distance quadratique entre deux trajectoires individuelles d'un même réseau, intégrée sur l'aléa, vaut à la limite thermodynamique :

$$(d^{(p)}(t))^{2}= \int \int \left(u_{i}^{(p)}(t)-{u_{i}^{(p)}}'(t)\right)^2 {dP_N^{(p)}}^2(t)$$

où $u_i^{(p)}(t)$ et ${u_i^{(p)}}'(t)$ sont deux trajectoires individuelles sur un même réseau issues de conditions initiales différentes.

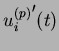Cependant, on a vu que les observables macroscopiques peuvent entretenir une dynamique pour les temps longs dans ce modèle, et en particulier la variance de potentiels $\nu^{(p)}(t)$ ne converge pas nécessairement vers une valeur limite constante ${\nu^{(p)}}^*$ lorsque $t$ tend vers l'infini. Ainsi, la décomposition entre un processus constant et un bruit blanc gaussien n'est plus possible dans le modèle à deux populations. Néanmoins, la méthode de Derrida et Pomeau [86], fondée sur un calcul de la divergence entre deux trajectoires, reste valable.

On note $\Delta ^{(p)}(t)$ la covariance entre ces deux trajectoires. De la même façon que dans le modèle à une population, on obtient une expression générique de la distance quadratique à la limite thermodynamique :

Pour $p\in \{1,2\}$ et $1\leq t\leq T-1~$ :

$${d^{(p)}(t)}^{2}=2(\nu ^{(p)}(t)-\Delta ^{(p)}(t))$$ (2.7)

$$\Delta ^{(p)}(t+1)={\sigma_J^{(p1)}}^{2}C^{(1)}(t)+{\sigma_J^{(p2)}}^{2}C^{(2)}(t)+{\sigma _{\theta}^{(p)}}^{2}$$

avec

$$\hspace{-0.4cm}C^{(p)}(t)= \int \int Dh Dh'f\left(\frac{\sqrt{{\n... ...sqrt{\nu ^{(p)}(t)}}h'+\mu^{(p)}(t)\right)f(h'\sqrt{\nu^{(p)}(t)}+\mu^{(p)}(t))$$

Comme précédemment, le comportement de la distance quadratique nous permet de déterminer deux types de régimes à la limite thermodynamique, le passage de l'un à l'autre s'opérant par bifurcation. On dit que le régime dynamique est stable si la distance quadratique $(d^{(p)}(t))$ tend vers zéro quand $t$ tend vers l'infini. On parle de régime dynamique déstabilisé si $d^{(p)}(t)$ tend à augmenter au cours du temps. Comme précédemment, cette dynamique déstabilisée est associée à taille finie aux régimes de type chaotique.