Fonction de transfert et signaux non-centrés

À titre d'exemple, les schémas ci-dessous indiquent les déformations subies par un signal sinusoïdal lorsqu'on le passe par la fonction de transfert $f_g(x)=(1+\tanh(gx))/2$, avec $g=3$ :

• Signal sinusoïdal, moyenne 1, écart-type 0.35 :
  $\stackrel{f_g}{\longrightarrow}$
• Signal sinusoïdal, moyenne 0, écart-type 0.35 :
  $\stackrel{f_g}{\longrightarrow}$
• Signal sinusoïdal, moyenne -1, écart-type 0.35 :
  $\stackrel{f_g}{\longrightarrow}$

On constate immédiatement que les signaux non-centrés, dont les valeurs sont situées aux alentours de 1 ou de -1 pour cet exemple, se retrouvent ``aplatis'' par la fonction de transfert. Le signal de moyenne 1 produit un signal presque plat, prenant ses valeurs aux alentours de 1 (limite supérieure de la sortie de la fonction de transfert). Le signal de moyenne -1 produit un signal presque plat, prenant ses valeurs aux alentours de 0 (limite inférieure de la sortie de la fonction de transfert). Un signal dont les valeurs sont situées aux alentours de zéro subit une légre déformation, mais la sortie prend ses valeurs sur l'ensembles de l'intervalle ]0,1[. En général, plus la moyenne du signal considéré est excentrée, plus la fonction de transfert tend à aplatir le signal.

On peut ramener ces observations aux signaux produits par le réseau. Le signal de potentiel $u_i(t)$ est un signal non-centré, dont la moyenne est $u_i^*$ (potentiel moyen). Suivant la valeur du potentiel moyen, le signal $x_i(t)=f_g(u_i(t))$ n'aura pas les mêmes caractéristiques.

• Si la valeur de $u_i^*$ est proche de zéro, le neurone tend à propager son signal de potentiel. Ce neurone est dit actif.
• Si la valeur de $u_i^*$ est excentrée, le signal $x_i(t)$ est très écrasé, et son activité dynamique est faible. Ce neurone est dit figé.
  • Si l'activation reste proche de la valeur 0, le neurone est dit muet.
  • Si l'activation reste proche de la valeur 1, le neurone est dit saturé.

Ainsi, dans un réseau pour lequel les potentiels moyens peuvent prendre des valeurs excentrées, seul un sous-ensemble de neurones transmet le signal dynamique, et est réellement actif dans l'entretien de la dynamique qui se développe dans le réseau. La répartition des activations moyennes 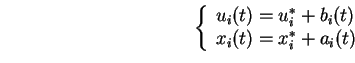$x_i^*$ et des potentiels moyen $u_i^*$ peut nous renseigner sur ces proportions.