


Next: Recognition, retrieval and dynamical
Up: Learning and retrieval
Previous: Learning and retrieval
Learning process
Let us now consider that the primary layer is continuously stimulated
by a periodic signal
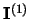 (repeated every
(repeated every  time steps), and the dynamics of the system is given by
(2).
Fig.3 presents the time evolution of
the neural activity in population 2 while the system is submitted
to a period-5 spatio-temporal input signal (for visual comfort, we
have taken a pattern representing a frog jump).
time steps), and the dynamics of the system is given by
(2).
Fig.3 presents the time evolution of
the neural activity in population 2 while the system is submitted
to a period-5 spatio-temporal input signal (for visual comfort, we
have taken a pattern representing a frog jump).
Figure 3:
Learning dynamics, between 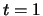 and
and 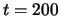 (with
(with
 ,
,  ). The system is continuously
stimulated by a periodic spatio-temporal pattern (a frog jump).
Parameters are in Tab.1. - a - Neuronal
activity on secondary layer. 30 individual signals (out of 200)
have been represented, and their mean activity is represented
below. - b - Time evolution of input signal
). The system is continuously
stimulated by a periodic spatio-temporal pattern (a frog jump).
Parameters are in Tab.1. - a - Neuronal
activity on secondary layer. 30 individual signals (out of 200)
have been represented, and their mean activity is represented
below. - b - Time evolution of input signal
 and feedback reinforcement
and feedback reinforcement
 (see text), between
(see text), between  and
and  (For
readability, most of the time steps have been discarded). At each
time step, the 1600 values have been represented as
(For
readability, most of the time steps have been discarded). At each
time step, the 1600 values have been represented as 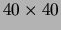 images, where white corresponds to 0 and black to 1 (in-between
values are gray tones).
images, where white corresponds to 0 and black to 1 (in-between
values are gray tones).
|
|
During the learning process, the synaptic weights are modified at each
time step, so that the whole system continuously evolves under the
constraint of the external signal
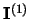 . Two sorts of
dynamical changes can thus be observed in the system (Fig.
3).
First, the secondary layer activity, which is initially chaotic,
gets closer to a periodic behavior (Fig.3-a-). The
learning process tends to reduce the complexity of the
initial chaotic dynamics towards a periodic dynamics (period-5
dynamics), so that the predictability between primary and
secondary layers activities tends to increase. Nevertheless,
changes on the weights remain very weak, and the statistics of the
weight matrix remains the same as the one of the initial random
matrix.
Second, at each time step,
a subset of neurons (
. Two sorts of
dynamical changes can thus be observed in the system (Fig.
3).
First, the secondary layer activity, which is initially chaotic,
gets closer to a periodic behavior (Fig.3-a-). The
learning process tends to reduce the complexity of the
initial chaotic dynamics towards a periodic dynamics (period-5
dynamics), so that the predictability between primary and
secondary layers activities tends to increase. Nevertheless,
changes on the weights remain very weak, and the statistics of the
weight matrix remains the same as the one of the initial random
matrix.
Second, at each time step,
a subset of neurons ( ) is active in secondary layer. The
rule strengthens the connections between the secondary layer
subset which was active at time
) is active in secondary layer. The
rule strengthens the connections between the secondary layer
subset which was active at time 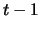 and the primary
neurons that are active at time
and the primary
neurons that are active at time  . This reinforcement of
feedback weights takes place at every time step, while the primary
layer is periodically stimulated. The effective feedback signal is
given by the local-field
. This reinforcement of
feedback weights takes place at every time step, while the primary
layer is periodically stimulated. The effective feedback signal is
given by the local-field
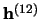 . During the first
steps of the learning process, the amplitude of this signal is
weak, which means that the feedback influence is almost
negligible. Then, as time goes on, the amplitude of the feedback
signal grows, and then some values of
. During the first
steps of the learning process, the amplitude of this signal is
weak, which means that the feedback influence is almost
negligible. Then, as time goes on, the amplitude of the feedback
signal grows, and then some values of
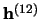 reach
the critical threshold value
reach
the critical threshold value  , and thus
significantly increase the activation of the corresponding primary
neurons. In order to estimate and represent the efficacy of this
feedback signal, we consider the signal
, and thus
significantly increase the activation of the corresponding primary
neurons. In order to estimate and represent the efficacy of this
feedback signal, we consider the signal
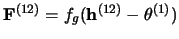 , which
corresponds to what would be the primary layer activation if no
input was sent. This signal is displayed on Fig.3-b-,
and compared with the current input signal
, which
corresponds to what would be the primary layer activation if no
input was sent. This signal is displayed on Fig.3-b-,
and compared with the current input signal
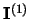 .
One can remark that the input signal and the feedback signal are
synchronized. Knowing that the transmission delay from secondary
towards primary layer is equal to 1, the feedback signal at time
.
One can remark that the input signal and the feedback signal are
synchronized. Knowing that the transmission delay from secondary
towards primary layer is equal to 1, the feedback signal at time
 relies on the secondary pattern of activation at time
relies on the secondary pattern of activation at time 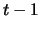 ,
so that the secondary layer anticipates the activity of
primary layer. The feedback signal is thus a prediction on the
forthcoming input, and corresponds to a ``top-down expectation''.
The signal
,
so that the secondary layer anticipates the activity of
primary layer. The feedback signal is thus a prediction on the
forthcoming input, and corresponds to a ``top-down expectation''.
The signal
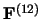 also provides an objective
criterion for stopping the learning process. When the value of the
feedback signal is of the order of the input signal, the learning
process can be stopped so that one can test the recognition
properties of the system (see next section). Note that the
unbounded continuation of the learning process increases too
strongly the amplitude of the feedback signal and the reduction of
the inner dynamics, so that the system becomes insensitive to its
input signal (and thus looses its adaptivity).
also provides an objective
criterion for stopping the learning process. When the value of the
feedback signal is of the order of the input signal, the learning
process can be stopped so that one can test the recognition
properties of the system (see next section). Note that the
unbounded continuation of the learning process increases too
strongly the amplitude of the feedback signal and the reduction of
the inner dynamics, so that the system becomes insensitive to its
input signal (and thus looses its adaptivity).



Next: Recognition, retrieval and dynamical
Up: Learning and retrieval
Previous: Learning and retrieval
Dauce Emmanuel
2003-04-08
![\includegraphics[width=15cm]{bc_fig2.eps}](img130.png)
![\includegraphics[width=15cm]{bc_fig2.eps}](img130.png)