


Next: ReST model
Up: Multi-population recurrent model
Previous: Activation dynamics
We extend here the activation dynamics to a generic on-line
learning dynamics. A first article [10] presented a Hebbian
learning process in a non-structured RRNN,
that was found to reduce the complexity of the
dynamics (later on called ``dynamics reduction''). We propose here
a local Hebbian learning rule that relies on an on-line
estimate of the covariance between afferent and efferent signals,
as in [31].
We will suppose hereafter that we have
at each time step local estimates of mean activation, which are
stored in vector
 , and updated according to
, and updated according to
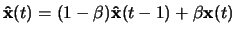 ,
and we take
,
and we take 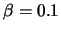 in our simulations.
The learning dynamics is thus described by the set of
equations:
in our simulations.
The learning dynamics is thus described by the set of
equations:
 |
(2) |
where
 is a function that prevents
weight drift when the post-synaptic neuron is saturated, and
is a function that prevents
weight drift when the post-synaptic neuron is saturated, and
 is the learning parameter from population
is the learning parameter from population  towards population
towards population  (supposed small).
Note that we take into
account the discrete time delay between pre-synaptic neuron
(supposed small).
Note that we take into
account the discrete time delay between pre-synaptic neuron 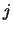 and post-synaptic neuron
and post-synaptic neuron  , which is important for learning
temporal dependencies [19].
, which is important for learning
temporal dependencies [19].



Next: ReST model
Up: Multi-population recurrent model
Previous: Activation dynamics
Dauce Emmanuel
2003-04-08
