


Next: Learning dynamics
Up: Multi-population recurrent model
Previous: Multi-population recurrent model
Our dynamical system (1) is defined as a pool of 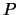 interacting populations of neurons, of respective sizes
interacting populations of neurons, of respective sizes  ,
...,
,
...,  . The global number of neurons is
. The global number of neurons is
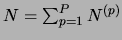 . The synaptic weights from population
. The synaptic weights from population  towards
population
towards
population  are stored in a matrix
are stored in a matrix
 of size
of size
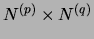 . The state vector of population
. The state vector of population  at
time
at
time  is
is
 , of size
, of size  . The initial
conditions
. The initial
conditions 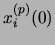 are set according to a random draw
uniform in
are set according to a random draw
uniform in ![$]0,1[$](img66.png) .
At each time step
.
At each time step 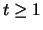 ,
,
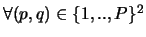 ,
,
 ,
,
is the local field of population  towards neuron
towards neuron  of population
of population  .
This variable measures the influence of a particular population
on the activity of a given neuron.
We also consider spatio-temporal input signals
.
This variable measures the influence of a particular population
on the activity of a given neuron.
We also consider spatio-temporal input signals
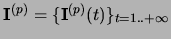 , where
, where
 is a
is a  dimensional input vector at
time
dimensional input vector at
time  on population
on population  . The input
. The input
 acts
like a bias on each neuron (on the contrary to Hopfield system,
the input doesn't correspond to the initial state
acts
like a bias on each neuron (on the contrary to Hopfield system,
the input doesn't correspond to the initial state 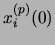 of the network). Then, the global equation of the dynamics is :
of the network). Then, the global equation of the dynamics is :
 |
(1) |
The activation potentials 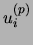 have real continuous values,
and correspond to a linear combination of afferent local fields
minus activation threshold
have real continuous values,
and correspond to a linear combination of afferent local fields
minus activation threshold 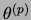 .
The activation states
.
The activation states  are continuous and take their
values in
are continuous and take their
values in ![$]0,1[$](img66.png) , with a nonlinear transfer function
, with a nonlinear transfer function
 , whose gain is
, whose gain is 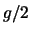 . We call
``pattern of activation'' the spatio-temporal signal
. We call
``pattern of activation'' the spatio-temporal signal
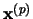 corresponding to the exhaustive description of
a trajectory of the system's dynamics in layer
corresponding to the exhaustive description of
a trajectory of the system's dynamics in layer  .
An important characteristics of our system is the random nature of
the connectivity pattern. We suppose that the distribution of the
connection weights follow the Gaussian law
.
An important characteristics of our system is the random nature of
the connectivity pattern. We suppose that the distribution of the
connection weights follow the Gaussian law
 , so that
, so that
 . This random draw implies that our
synaptic weights are almost surely non-symmetric. This
non-symmetry is a necessary requirement for having complex
dynamics.
As the local fields
. This random draw implies that our
synaptic weights are almost surely non-symmetric. This
non-symmetry is a necessary requirement for having complex
dynamics.
As the local fields 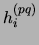 are updated synchronously, the
global dynamics (1) also obeys to a synchronous update.
Then, the state of the system at time
are updated synchronously, the
global dynamics (1) also obeys to a synchronous update.
Then, the state of the system at time  both depends on the
state of the system at time
both depends on the
state of the system at time 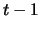 and the input
and the input  (at time
(at time  ). One can thus notice that (i) the transmission delay
is uniformly equal to 1, (ii) our system is deterministic as soon
as the input signal is set according to a deterministic process.
). One can thus notice that (i) the transmission delay
is uniformly equal to 1, (ii) our system is deterministic as soon
as the input signal is set according to a deterministic process.



Next: Learning dynamics
Up: Multi-population recurrent model
Previous: Multi-population recurrent model
Dauce Emmanuel
2003-04-08

