


Next: Capacity
Up: Recognition, retrieval and dynamical
Previous: Retrieval
One major interest of our system is its capacity to learn numerous
different spatio-temporal patterns (see sect. 4.3).
Learning to recognize several spatio-temporal stimuli can lead to
ambiguous situations, in particular when distinct input sequences
have common features. In that case, some input signals are
spatially ambiguous, i.e. they can be interpreted as belonging to
two different sequences.
Figure:
Dynamical memory (Feedback retrieval depends on the past
of the dynamics). Two
sequences (
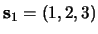 ,
,
 ),
whose common element is ``3'', have been learned.
),
whose common element is ``3'', have been learned.
 is presented between
is presented between 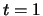 and
and 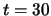 ,
,
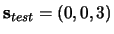 is presented between
is presented between
 and
and  ,
,
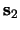 is presented between
is presented between 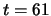 and
and 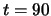 , and
, and
 is presented between
is presented between 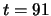 and
and 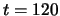 .
.
 ,
,  , other parameters are in
Tab.1.
- a -
Neuronal activity on secondary layer. 20
individual signals are represented, with their
mean activity.
- b -
Input (I) and Feedback (F) signals. Only the values corresponding to
the five first primary neurons are represented
between
, other parameters are in
Tab.1.
- a -
Neuronal activity on secondary layer. 20
individual signals are represented, with their
mean activity.
- b -
Input (I) and Feedback (F) signals. Only the values corresponding to
the five first primary neurons are represented
between  and
and 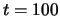 (some time steps have been discarded
for readability).
(some time steps have been discarded
for readability).
|
|
Fig.6 presents a system which has learned two distinct
sequences :
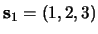 and
and
 .
These two sequences are 3-periodic and have in common the element
``3''. The figure shows that the way the same dynamical
sequence, i.e.
.
These two sequences are 3-periodic and have in common the element
``3''. The figure shows that the way the same dynamical
sequence, i.e.
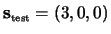 is
interpreted depends on previous stimulations: when the system is
stimulated by sequence
is
interpreted depends on previous stimulations: when the system is
stimulated by sequence  , it reaches an attractor
associated to
, it reaches an attractor
associated to  and interprets
and interprets
 as
as  . When
. When
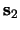 is presented, the system changes its basin of
attraction and reaches the one associated to
is presented, the system changes its basin of
attraction and reaches the one associated to 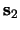 , so
that
, so
that
 is now interpreted as
is now interpreted as
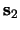 . In that particular example, one can remark that
the time necessary to reach the second attractor is rather long,
i.e. the presentation of the second stimulus during 30 time steps
(from
. In that particular example, one can remark that
the time necessary to reach the second attractor is rather long,
i.e. the presentation of the second stimulus during 30 time steps
(from 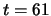 to
to 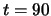 ) is just long enough for stabilizing the
response of the system on the second attractor.
Particularly interesting is the global remapping one can
observe in the secondary layer (Fig.6-a-). The change
in the inner organization is perceptible around
) is just long enough for stabilizing the
response of the system on the second attractor.
Particularly interesting is the global remapping one can
observe in the secondary layer (Fig.6-a-). The change
in the inner organization is perceptible around  (20 steps
after the presentation of
(20 steps
after the presentation of  ), and one can see that the
activity of the secondary neurons change qualitatively (some
neurons become silent, other become more active). This different
inner organization explains that one can have different feedback
response when the same stimulus
), and one can see that the
activity of the secondary neurons change qualitatively (some
neurons become silent, other become more active). This different
inner organization explains that one can have different feedback
response when the same stimulus
 is presented. So, this example shows that the way a given signal
is presented. So, this example shows that the way a given signal
 is interpreted does not only
depend on its own intrinsic values, but also depends on a context
that can be memorized in an attractor. In that sense, our system
has a memory of past events.
is interpreted does not only
depend on its own intrinsic values, but also depends on a context
that can be memorized in an attractor. In that sense, our system
has a memory of past events.
So, we have shown that after learning one or several stimuli, our
system exhibits new computational abilities: the ability to
discriminate between familiar and unknown stimuli, the ability to
recognize and retrieve partial signals, and the ability to store
in the dynamics the memory of past events. Those properties are
grounded on the temporal behavior of the system, and for that
reason they are highly sensitive to the time relationships and to
the periodicity of the presented stimuli. Because they rely on a
dynamical system, they also need several time steps for the system
to converge towards its attractor, and the response at a given
time is not only guided by the input, but also by inner dynamical
constraints.
So, one can say that the computational abilities of
our systems are astonishingly complex, knowing that we start from a
rather simple design. One can now ask the question of capacity,
i.e. how many stimuli can be stored and retrieved in a single
system?



Next: Capacity
Up: Recognition, retrieval and dynamical
Previous: Retrieval
Dauce Emmanuel
2003-04-08
![\includegraphics[width=17cm]{bc_memory.eps}](img155.png)
![\includegraphics[width=17cm]{bc_memory.eps}](img155.png)