


Next: Robot experiment
Up: Learning and retrieval
Previous: Dynamical memory
Capacity
The number of different spatial input patterns that can be
memorized in recurrent attractor systems, like Hopfield systems,
is generally found to be linearly dependent in  . One thus
defines a capacity criterion
. One thus
defines a capacity criterion
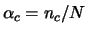 where
where  is
the maximal ``critical'' number of spatial patterns that can be
learned. For a given value of
is
the maximal ``critical'' number of spatial patterns that can be
learned. For a given value of  , when one tries to learn more
than
, when one tries to learn more
than  spatial patterns, the retrieval ability suddenly
decreases (``catastrophic'' forgetting).
Starting from a tabula rasa, one can also store spatio-temporal periodic
patterns instead of
spatial patterns in recurrent systems [19].
Basically, individual neurons work as coincidence detectors, and tend
to react specifically to the co-activation of a given set of pre-synaptic
neurons. Globally, one can observe chains of firing, leading to a stable
spatio-temporal activation pattern [17].
In case such chains are closed, every different loop
corresponds to a different periodic (cyclic) attractor.
The capacity of such systems obey to the same constraints as Hopfield
systems, and is also defined as the number of spatial
patterns that can be stored, independently of their temporal succession.
Theoretical estimates of the capacity of such systems can be found in
[24,17].
In our systems, there is no explicit storage of spatio-temporal
sequences. The retrieval relies on two mechanisms: (i) the
decrease of chaos (i.e. increase of predictability) between
primary and secondary layers activities (which is necessary for
the robustness of the response) and (ii) a coincidence detection
mechanism from secondary layer towards primary layer (which
activates or disables feedback signal). In order to allow
comparison with existing models, we define a measure of capacity
that relies on this retrieval mechanism. The ``knowledge'' of a
given sequence of inputs thus manifests in the network ability to
activate a feedback signal which is coherent with the input
signal. For an estimation of the capacity, we only refer to the
size of the secondary layer
spatial patterns, the retrieval ability suddenly
decreases (``catastrophic'' forgetting).
Starting from a tabula rasa, one can also store spatio-temporal periodic
patterns instead of
spatial patterns in recurrent systems [19].
Basically, individual neurons work as coincidence detectors, and tend
to react specifically to the co-activation of a given set of pre-synaptic
neurons. Globally, one can observe chains of firing, leading to a stable
spatio-temporal activation pattern [17].
In case such chains are closed, every different loop
corresponds to a different periodic (cyclic) attractor.
The capacity of such systems obey to the same constraints as Hopfield
systems, and is also defined as the number of spatial
patterns that can be stored, independently of their temporal succession.
Theoretical estimates of the capacity of such systems can be found in
[24,17].
In our systems, there is no explicit storage of spatio-temporal
sequences. The retrieval relies on two mechanisms: (i) the
decrease of chaos (i.e. increase of predictability) between
primary and secondary layers activities (which is necessary for
the robustness of the response) and (ii) a coincidence detection
mechanism from secondary layer towards primary layer (which
activates or disables feedback signal). In order to allow
comparison with existing models, we define a measure of capacity
that relies on this retrieval mechanism. The ``knowledge'' of a
given sequence of inputs thus manifests in the network ability to
activate a feedback signal which is coherent with the input
signal. For an estimation of the capacity, we only refer to the
size of the secondary layer  , as the size of primary
layer has no influence on the retrieval properties of the system.
During the training process, a spatio-temporal sequence
, as the size of primary
layer has no influence on the retrieval properties of the system.
During the training process, a spatio-temporal sequence  is repeatedly presented until our learning mechanism (2)
produces an active feedback signal.
Then, we test the correlation between input and feedback signals
for that particular sequence (with dynamics (1)), i.e.
is repeatedly presented until our learning mechanism (2)
produces an active feedback signal.
Then, we test the correlation between input and feedback signals
for that particular sequence (with dynamics (1)), i.e.
 and
and
 , with
, with  . If
. If
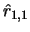 is close to 1, input and feedback signals are
found to overlap. Then a second sequence is learned, then a third
one, ..., then a
is close to 1, input and feedback signals are
found to overlap. Then a second sequence is learned, then a third
one, ..., then a  one... The period of the
one... The period of the  sequence is chosen between 3 and 7, i.e
sequence is chosen between 3 and 7, i.e
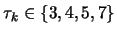 ,
with equal probability. At step
,
with equal probability. At step  , we measure the retrieval for
every previously learned sequence, i.e for
, we measure the retrieval for
every previously learned sequence, i.e for 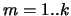 , we calculate
, we calculate
 . For every value of
. For every value of  , the total number of
spatial patterns that compose the learned sequences is equal to
, the total number of
spatial patterns that compose the learned sequences is equal to
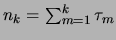 . The mean retrieval among all learned
sequences is equal to
. The mean retrieval among all learned
sequences is equal to
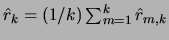 .
When
.
When  is close to one, the retrieval is good for almost
every sequence. When
is close to one, the retrieval is good for almost
every sequence. When  is close to zero, the ability to
retrieve any of the learned sequences is null, which corresponds
to a ``catastrophic forgetting''.
is close to zero, the ability to
retrieve any of the learned sequences is null, which corresponds
to a ``catastrophic forgetting''.
Figure:
Different measures of the capacity of the model.
 is plotted in function of
is plotted in function of 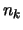 (see text).
Non-specified parameters are in Tab. 1.
- a -
Inter-individual variability, in case of elementary sequences
learning, with
(see text).
Non-specified parameters are in Tab. 1.
- a -
Inter-individual variability, in case of elementary sequences
learning, with
 ,
,
 and
and
 .
Dotted lines correspond to individual networks, plain line corresponds to
the mean over the 10 networks.
- b -
Measures of capacity for different values of
.
Dotted lines correspond to individual networks, plain line corresponds to
the mean over the 10 networks.
- b -
Measures of capacity for different values of
 , in case of elementary sequences
learning, with
, in case of elementary sequences
learning, with
 , and
, and  .
- c -
Measures of capacity for different values of
.
- c -
Measures of capacity for different values of  ,
in case of elementary sequences
learning, with
,
in case of elementary sequences
learning, with
 and
and
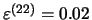 .
- d -
Measures of capacity for different values of input sparsity
.
- d -
Measures of capacity for different values of input sparsity  ,
with
,
with
 ,
,
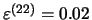 and
and
 .
.
|
|
This experiment has been carried out on 10 networks
(Fig.7-a-) with elementary sequences (and without
overlap between the spatial patterns composing the sequences). The
size of secondary layer is  and learning only takes
place on feedback links (i.e.
and learning only takes
place on feedback links (i.e.
 ). For every
network,
). For every
network,  is plotted in function of
is plotted in function of 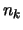 . Globally,
the shape of the curves is similar for every network, with good
retrieval for low values of
. Globally,
the shape of the curves is similar for every network, with good
retrieval for low values of 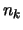 , and a sudden decrease towards
zero. So, one can estimate, for a given network, a critical value
, and a sudden decrease towards
zero. So, one can estimate, for a given network, a critical value
 (corresponding to the sudden decrease) so that
(corresponding to the sudden decrease) so that
 . There are sensitive differences between
individual networks (i.e.
. There are sensitive differences between
individual networks (i.e.  is between 120 and 180), and the
mean capacity
is between 120 and 180), and the
mean capacity  is found to be of the order of 0.7.
The shape of the curves and the value of
is found to be of the order of 0.7.
The shape of the curves and the value of  strongly vary
depending on the parameters settings. We have tried on
the following experiments to estimate the role of
strongly vary
depending on the parameters settings. We have tried on
the following experiments to estimate the role of
 (inner links learning parameter Fig.
7-b-),
(inner links learning parameter Fig.
7-b-),  (size of secondary layer Fig.
7-c-) and
(size of secondary layer Fig.
7-c-) and  (spatial input patterns
sparsity Fig.7-d-).
Parameter
(spatial input patterns
sparsity Fig.7-d-).
Parameter
 relates to the process of dynamics
reduction. The more
relates to the process of dynamics
reduction. The more
 is high, the less chaotic
(more predictable) is the response of the system after learning.
The link between this increase of predictability and the increase
of robustness to noise has been shown in simpler learning
situations ([10]). It has also been shown that this
increase of robustness is costly, i.e. an increase of robustness
induces a decrease of capacity. The same dilemma holds on the
present model. We can see on Fig.7-b- that an
increase of parameter
is high, the less chaotic
(more predictable) is the response of the system after learning.
The link between this increase of predictability and the increase
of robustness to noise has been shown in simpler learning
situations ([10]). It has also been shown that this
increase of robustness is costly, i.e. an increase of robustness
induces a decrease of capacity. The same dilemma holds on the
present model. We can see on Fig.7-b- that an
increase of parameter
 has a counterpart in
terms of capacity. The more stable is the response, the lower is
the capacity. One has to find a compromise between stability and
capacity. For the experiments carried out in the previous section,
we have taken
has a counterpart in
terms of capacity. The more stable is the response, the lower is
the capacity. One has to find a compromise between stability and
capacity. For the experiments carried out in the previous section,
we have taken
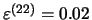 , which corresponds to a
capacity of the order of 0.5.
The size effects are displayed on Fig.7-c-, again
with elementary sequences and
, which corresponds to a
capacity of the order of 0.5.
The size effects are displayed on Fig.7-c-, again
with elementary sequences and
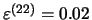 , with
different values of
, with
different values of  . With small fluctuations from one
network to the other, we find again a capacity of the order of
0.5.
At last, we measured the effect of cross-overlap between spatial
patterns composing the sequences. The spatial input patterns are
supposed sparse (i.e a small proportion of primary neurons are
stimulated at the same time), so that cross-overlap between
spatial input patterns is weak. When we use elementary sequences,
this cross-overlap is null. On Fig. 7 - d -, we
measure the capacity in case spatial input patterns are chosen
according to a random draw, so that
. With small fluctuations from one
network to the other, we find again a capacity of the order of
0.5.
At last, we measured the effect of cross-overlap between spatial
patterns composing the sequences. The spatial input patterns are
supposed sparse (i.e a small proportion of primary neurons are
stimulated at the same time), so that cross-overlap between
spatial input patterns is weak. When we use elementary sequences,
this cross-overlap is null. On Fig. 7 - d -, we
measure the capacity in case spatial input patterns are chosen
according to a random draw, so that
 and
and
 . In that case, the
cross-overlap between spatial patterns is of the order of
. In that case, the
cross-overlap between spatial patterns is of the order of
 . Fig.7-d- shows that cross
overlap induces a sensible decrease of capacity. For instance,
when
. Fig.7-d- shows that cross
overlap induces a sensible decrease of capacity. For instance,
when
 (which approximately corresponds to the
"frog" sequence of Fig.2), the capacity is of the order of 0.3
(i.e., when
(which approximately corresponds to the
"frog" sequence of Fig.2), the capacity is of the order of 0.3
(i.e., when  , the system should be able to learn and
discriminate of the order of 8 spatio-temporal sequences analogous
(statistically) to the frog sequence).
These experiments have shown that our system can display high
capacity (of the order of 0.7) in the best case, but real world
systems both need reliability of response and robustness to noise
and cross-overlap. Under these more realistic constraints, the
capacity of our system is found to be of the order of 0.3. We ask
in next section the question of real-world implementation, in case
of sensory-motor associations on a robotic task.
, the system should be able to learn and
discriminate of the order of 8 spatio-temporal sequences analogous
(statistically) to the frog sequence).
These experiments have shown that our system can display high
capacity (of the order of 0.7) in the best case, but real world
systems both need reliability of response and robustness to noise
and cross-overlap. Under these more realistic constraints, the
capacity of our system is found to be of the order of 0.3. We ask
in next section the question of real-world implementation, in case
of sensory-motor associations on a robotic task.



Next: Robot experiment
Up: Learning and retrieval
Previous: Dynamical memory
Dauce Emmanuel
2003-04-08
![\includegraphics[width=15cm]{bc_fig_capacite.eps}](img183.png)
![\includegraphics[width=15cm]{bc_fig_capacite.eps}](img183.png)