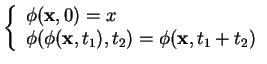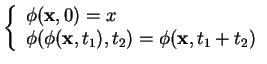suivant: Espace temporel
monter: Systèmes dynamiques
précédent: Systèmes dynamiques
Un système dynamique est défini par un triplet
 , constitué de l'espace d'états
, constitué de l'espace d'états  , du domaine temporel
, du domaine temporel  et d'une fonction de transition d'état
et d'une fonction de transition d'état
 , qui possède la propriété :
Pour tout
, qui possède la propriété :
Pour tout
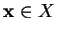 et
et
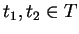 ,
,
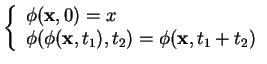 |
(1) |
A partir d'un vecteur de conditions initiales
 , la
fonction
, la
fonction  permet de définir l'état du système à tout instant.
Plus précisément, pour tout
permet de définir l'état du système à tout instant.
Plus précisément, pour tout
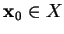 , la trajectoire
qui a
, la trajectoire
qui a
 pour origine est définie par l'application
pour origine est définie par l'application
 telle que
telle que
 .
Une trajectoire associe donc à chaque instant un point dans l'espace
d'états ; l'ensemble de ces points constitue une courbe appelée
orbite de
.
Une trajectoire associe donc à chaque instant un point dans l'espace
d'états ; l'ensemble de ces points constitue une courbe appelée
orbite de
 .
Le terme « trajectoire » évoque le déplacement d'un mobile au sein
d'un espace tridimensionnel.
Bien entendu, les variables d'état peuvent représenter bien autre
chose que des coordonnées spatiales, mais l'évolution de notre système
peut toujours être décrite par une courbe
au sein de son espace d'état (également appelé espace
des phases). Cette courbe fournit une représentation abstraite de
l'évolution du système.
.
Le terme « trajectoire » évoque le déplacement d'un mobile au sein
d'un espace tridimensionnel.
Bien entendu, les variables d'état peuvent représenter bien autre
chose que des coordonnées spatiales, mais l'évolution de notre système
peut toujours être décrite par une courbe
au sein de son espace d'état (également appelé espace
des phases). Cette courbe fournit une représentation abstraite de
l'évolution du système.
Dauce Emmanuel
2003-04-02