Influence du régime dynamique sur la configuration spatiale

On montre ici que les valeurs des $u_i^*$ dépendent peu du paramètre de gain $g$, ce qui signifie que la configuration spatiale dépend faiblement du régime dynamique.

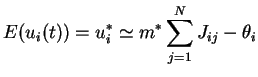Le tableau 3.1 donne, sur un réseau de 200 neurones, la corrélation entre ${u^*}^{(g)}$ et ${u^*}^{(\infty )}$, où ${u^*}^{(g)}$ est le vecteur des potentiels moyens pour le gain $g$ et ${u^*}^{(\infty )}$ donne le vecteur des potentiels moyens pour $g=\infty$, c'est à dire pour une fonction de transfert binaire.

Tableau 3.1: Corrélation entre ${u^*}^{(g)}$ et ${u^*}^{(\infty )}$, pour différentes valeurs de $g$, calculées sur un réseau en $[0,1]$, $N=200$.

g	0	1	2	3	4	5	10	15	20
cor$({u^*}^{(g)},{u^*}^{(\infty)})$	0.782	0.942	0.992	0.994	0.982	0.984	0.992	0.989	0.994

On voit ainsi qu'au delà de $g=2$, le vecteur des potentiels moyens $u^*$ est stabilisé, et reste fortement autocorrélé aux alentours de 0,99. On peut par extension dire que pour $g>2$, la configuration spatiale ne change pas, que le réseau soit en régime de point fixe, en régime cyclique ou en régime chaotique.

La configuration spatiale apparaît donc comme indépendante du régime dynamique. Elle caractérise l'organisation profonde du réseau. On peut la considérer comme un socle à partir duquel la dynamique se développe, sans l'affecter en retour.

À l'inverse, le paragraphe suivant montre qu'une modification des seuils a des conséquences très importantes sur la configuration spatiale.