L'estimation de ![]() donnée en (3.2) fait également intervenir la valeur locale du seuil
donnée en (3.2) fait également intervenir la valeur locale du seuil ![]() dont on a peu parlé jusqu'à présent.
Au signe près, le rôle du seuil
dont on a peu parlé jusqu'à présent.
Au signe près, le rôle du seuil ![]() est en fait tout à fait similaire à celui d'une entrée statique gaussienne
est en fait tout à fait similaire à celui d'une entrée statique gaussienne ![]() (de moyenne
(de moyenne ![]() et d'écart-type
et d'écart-type ![]() ).
La différence entre
).
La différence entre ![]() et
et ![]() repose plutôt sur l'interprétation de ces deux grandeurs : le motif statique est une modulation externe du champ local, tandis que le seuil est une modulation considérée comme ``interne''.
Les résultats qui suivent, qui portent sur l'influence de motifs statiques gaussiens sur la configuration spatiale, sont donc directement transposable aux seuils.
repose plutôt sur l'interprétation de ces deux grandeurs : le motif statique est une modulation externe du champ local, tandis que le seuil est une modulation considérée comme ``interne''.
Les résultats qui suivent, qui portent sur l'influence de motifs statiques gaussiens sur la configuration spatiale, sont donc directement transposable aux seuils.
Si l'on considère la dynamique contrainte par un motif ![]() gaussien, l'estimation d'
gaussien, l'estimation d'![]() à partir de
à partir de ![]() devient :
devient :
Ce n'est pourtant pas exactement ce qui se passe. En effet, la présentation d'un motif crée une perturbation dans les interactions entre neurones qui ne se ``résout'' qu'à l'issue du temps de relaxation. La nouvelle configuration dépend aussi du nouvel équilibre qui s'instaure entre les neurones. Le système étant non-linéaire, on peut dans tous les cas s'attendre à un nouveau vecteur des potentiels qui s'éloigne dans une certaine mesure de la simple addition entre le vecteur initial et le motif.
On va ici chercher à évaluer un peu plus précisément la nature de cette reconfiguration.
Suivant le choix des paramètres ![]() et
et ![]() , l'``impact'' du motif sur la dynamique du réseau sera plus ou moins important.
, l'``impact'' du motif sur la dynamique du réseau sera plus ou moins important.
Soit un réseau défini par le tirage de ses poids synaptiques et de ses seuils. On cherche à mesurer deux choses :
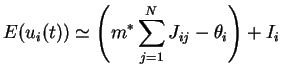 cor
corOn peut voir que si l'influence interne est forte et la discrimination faible, le réseau fournit une réponse qui dépend peu de son entrée. À l'inverse, si l'influence interne est faible et la discrimination forte, le réseau se contente de reproduire sur son vecteur des potentiels les caractéristiques de l'entrée. On peut dire dans ce cas que la configuration spatiale du réseau est ``contrôlée'' par le motif.
En observant le comportement des grandeurs ![]() et
et ![]() dans l'espace des paramètres, on cherche les valeurs de paramètres optimales telles que l'on maximise à la fois l'influence interne et la discrimination.
dans l'espace des paramètres, on cherche les valeurs de paramètres optimales telles que l'on maximise à la fois l'influence interne et la discrimination.
Pour estimer le comportement de ces grandeurs dans l'espace des paramètres, on a mesuré les quantités ![]() et
et ![]() , sur
, sur ![]() réseaux pour chaque valeur des paramètres
réseaux pour chaque valeur des paramètres ![]() (moyenne du motif) et
(moyenne du motif) et ![]() (écart-type du motif). La taille des réseaux est
(écart-type du motif). La taille des réseaux est ![]() et
et ![]() .
Les motifs étant tirés selon une loi gaussienne, ils sont comparables à des seuils additionnels.
Les résultats de cette mesure sont présentés figure 3.3.
.
Les motifs étant tirés selon une loi gaussienne, ils sont comparables à des seuils additionnels.
Les résultats de cette mesure sont présentés figure 3.3.
![\includegraphics[]{mesh_D.eps}](img717.png) ![\includegraphics[]{mesh_produitCD.eps}](img718.png) |
On voit clairement qu'influence interne et discrimination tendent à se comporter de manière complémentaire. Une influence interne élevée correspond généralement à une discrimination faible, et vice-versa.
De façon prévisible, des motifs de faible écart-type (
 ) sont mal discriminés (les caractéristiques spatiales de la dynamique spontanée l'emportent), tandis que des motifs de fort écart-type sont bien discriminés (les caractéristiques spatiales du motif l'emportent).
On constate que c'est pour des valeurs de l'ordre de
) sont mal discriminés (les caractéristiques spatiales de la dynamique spontanée l'emportent), tandis que des motifs de fort écart-type sont bien discriminés (les caractéristiques spatiales du motif l'emportent).
On constate que c'est pour des valeurs de l'ordre de
![]() que l'on observe un croisement des deux tendances, et où influence interne et influence externe s'équilibrent.
que l'on observe un croisement des deux tendances, et où influence interne et influence externe s'équilibrent.
La qualité du compromis entre influence interne et discrimination peut être mise en évidence par le produit ![]() .
On voit sur la figure 3.3 que la valeur de ce produit n'est pas uniforme dans l'espace des paramètres.
Si l'influence interne ou la discrimination sont très faibles, la valeur du produit sera proche de zéro.
Une valeur élevée de ce produit correspond à un bon équilibre entre les deux tendances.
On trouve, sur les données présentées, une valeur maximale du produit pour les paramètres (
.
On voit sur la figure 3.3 que la valeur de ce produit n'est pas uniforme dans l'espace des paramètres.
Si l'influence interne ou la discrimination sont très faibles, la valeur du produit sera proche de zéro.
Une valeur élevée de ce produit correspond à un bon équilibre entre les deux tendances.
On trouve, sur les données présentées, une valeur maximale du produit pour les paramètres (
![]() ,
,
![]() ), pour lesquels l'influence interne vaut 0.41 et la discrimination 0.71.
), pour lesquels l'influence interne vaut 0.41 et la discrimination 0.71.
La figure 3.4 représente les potentiels pour un motif dont la répartition obéit à une loi gaussienne et dont on a disposé les valeurs spatialement en faisant ressortir la diagonale pour faciliter l'interprétation visuelle
3.1.
On constate que l'augmentation du paramètre ![]() rend la diagonale plus visible sur les potentiels moyens, ce qui correspond à une augmentation de la corrélation entre
rend la diagonale plus visible sur les potentiels moyens, ce qui correspond à une augmentation de la corrélation entre ![]() et
et ![]() .
.
|
|
Donc, plus on augmente ![]() , plus le motif intervient fortement pour déterminer la configuration spatiale.
Néanmoins, on peut remarquer comme dans le paragraphe précédent qu'une corrélation de l'ordre 0.6 entre le motif
, plus le motif intervient fortement pour déterminer la configuration spatiale.
Néanmoins, on peut remarquer comme dans le paragraphe précédent qu'une corrélation de l'ordre 0.6 entre le motif ![]() et le vecteur des potentiels moyens
et le vecteur des potentiels moyens ![]() autorise des écarts importants entre les deux jeux de valeurs ; ces écarts, amplifiés par la non-linéarité de la fonction de transfert, aboutissent à des répartitions entre neurones actifs et neurones figés qui dépendent en fin de compte faiblement des valeurs précises du motif
autorise des écarts importants entre les deux jeux de valeurs ; ces écarts, amplifiés par la non-linéarité de la fonction de transfert, aboutissent à des répartitions entre neurones actifs et neurones figés qui dépendent en fin de compte faiblement des valeurs précises du motif ![]() et dépendent fortement des interactions qui prennent place entre les neurones au cours de la dynamique.
et dépendent fortement des interactions qui prennent place entre les neurones au cours de la dynamique.
On a donc principalement deux résultats :
Sachant que la configuration spatiale a une influence importante sur les caractéristiques de la dynamique (valeur de déstabilisation), il reste à regarder dans quelle mesure la reconfiguration spatiale issue de la présentation d'un motif agit sur la dynamique du réseau.
Avant cela, on va tenter de préciser la nature de l'organisation dynamique.