Discrimination dynamique

Considérons un réseau destabilisé (en régime cyclique ou chaotique) auquel on présente un motif statique. cela revient à modifier soudainement les paramètres du système. Le système se retrouve hors d'équilibre et converge vers un nouvel attracteur. L'importance de ces changements dépend de la moyenne et de la dispersion des valeurs du motif. On comprend en effet que plus les valeurs des motifs sont variées, et élevées en valeur absolue, plus le nouveau système est loin de l'équilibre et plus le nouvel attracteur sera éloigné de l'attracteur initial.

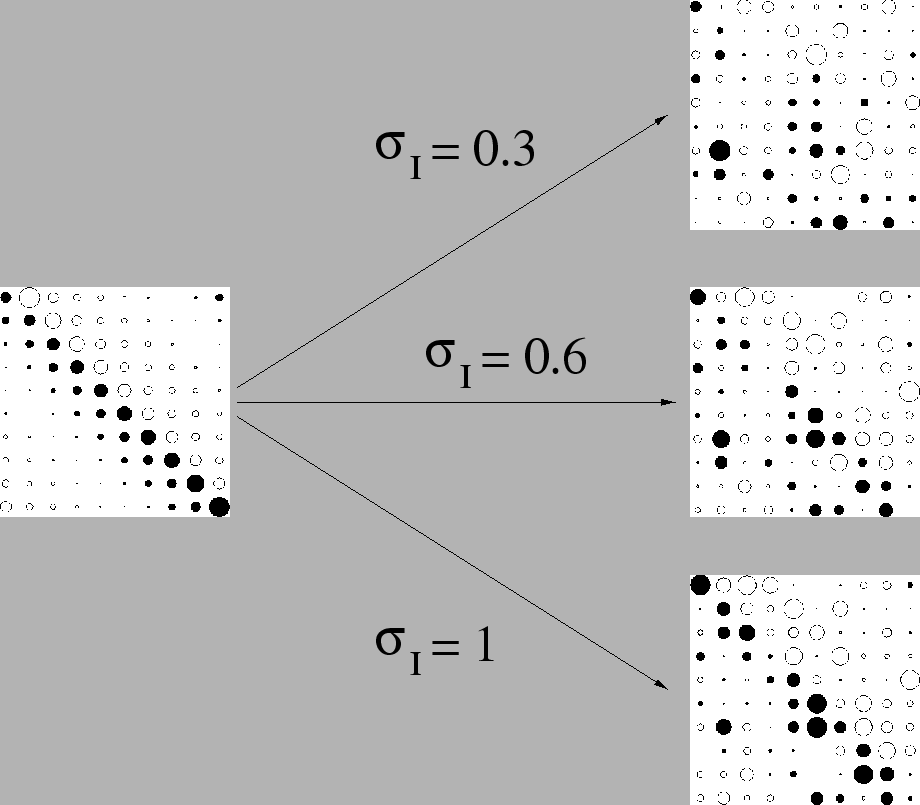
Dans le cas de motifs tirés selon une loi gaussienne identique, les différents jeux de valeurs peuvent induire des réponses dynamiques très différentes. Certains de ces motifs font augmenter l'activité dynamique du réseau, et la complexité de la dynamique. D'autres motifs, analogues statistiquement, tendent au contraire à diminuer l'activité dynamique du réseau, voire à l'éteindre complètement. Le réseau fournit une réponse dynamique différente dans les deux cas présentés, et opère donc une discrimination dynamique entre les deux motifs.

On a représenté sur la figure 3.19 différentes réponses dynamiques pour un même réseau, avec des motifs tirés suivant la même loi.

Si on s'intéresse statistiquement aux réponses dynamiques moyennes, pour des dynamiques spontanées telles que $\bar{\theta}=0$, $\sigma _\theta =0$, et des motifs aléatoires de moyenne $\bar{I}=0$ et d'écart-type $\sigma _I$, on observe les tendances suivantes [94] :

• Quelle que soit la valeur de $\sigma _I$, la tendance majoritaire est la diminution de l'activité dynamique (l'amplitude du signal $m_N(t)$ diminue).
• Plus la perturbation est importante (plus $\sigma _I$ est élevé), plus la proportion de motifs qui réduisent la dynamique augmente.

Ces tendances sont une fois de plus corroborées par le comportement du système à la limite thermodynamique.

Figure 3.19: Trois exemples de réponses dynamiques sur un même réseau. Les trois figures présentent l'évolution du signal $m_N(t)$ au cours du temps. Les 100 premiers pas de temps correspondent à la dynamique spontanée (en régime stationnaire). Les 100 pas de temps suivants correspondent à la dynamique contrainte, pour trois motifs différents tirés selon la même loi gaussienne. La dynamique spontanée est légèrement chaotique. Le premier motif (haut) mène à une augmentation de l'activité dynamique (augmentation de l'amplitude) avec augmentation de la complexité. Le second motif mène à une diminution de l'activité dynamique, et diminution de la complexité (on passe à un régime de cycle limite). Le troisième motif mène à une complète extinction de la dynamique. Paramètres : $N=100$, $g=6$, $\bar{J}=0$, $\sigma _J=1$, $\bar{\theta}=0$, $\sigma _\theta =0$, $\bar{I}=0$, $\sigma _I=0.3$.