Comportement statistique de la covariance

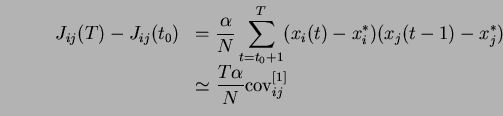
Une loi de puissance est caractérisée par une densité de la forme :

$$f(x)=B x^{-b}$$

avec $b>1$. Plus la valeur de $b$ est élevée, plus la probabilité associée à un événement de grande amplitude est faible. Les lois de puissance caractérisent des répartitions fortement hétérogènes, pour lesquelles un très petit nombre d'observables portent l'essentiel de l'énergie (ou une autre mesure) du système. La valeur de l'exposant indique le degré d'hétérogénéité de la distribution. Plus l'exposant est élevé, moins la distribution est homogène.

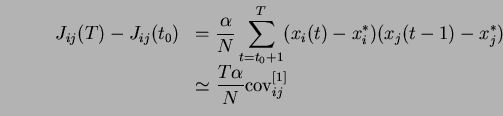
D'un point de vue pratique, étant donnée un jeu de mesures $m=\{m_i\}_{i=1..N}$, on pourra dire que cet ensemble obéit à une loi de puissance si la répartition empirique manifeste une linéarité en échelle (Log,Log). La pente de cette répartition empirique nous fournit l'exposant $b$.

On a représenté sur la figure 4.1 la répartition empirique des valeurs absolues des covariances cov$_{ij}^{[1]}$ mesurées sur un même réseau pour un régime pseudo-périodique ($g=4.2$) et un régime chaotique ($g=5$). Dans les deux cas, on voit apparaître en échelle (Log,Log) une série de points alignés, puis un phénomène de ``cut-off'' classique lié à la taille finie de l'échantillon. On trouve dans le premier cas (cycle limite) $b \simeq 1,37$ et dans le second (chaos) $b \simeq 1,09$. La dynamique chaotique manifeste donc une homogénéité plus grande (relativement) sur sa distribution des covariances. Cela indique simplement que les neurones actifs sont plus nombreux proportionnellement dans le second cas.

Figure: Loi de puissance sur la valeur absolue de la covariance des activations. La mesure est faite sur un réseau de 200 neurones en dynamique stationnaire. On a tracé l'histogramme de la valeur absolue de la covariance cov$_{ij}^{[1]}$. Abcisse et ordonnée sont en échelle logarithmique. Figure de gauche : régime pseudo-périodique ($g=4.2$). La pente est $b \simeq 1,37$. Figure de droite : régime chaotique ($g=5$). La pente est $b \simeq 1,09$. Paramètres : $\bar{\theta}=0$, $\sigma _{\theta }=0$, $\bar{J}=0$, $\sigma _J=1$.

On voit de façon manifeste qu'un terme de covariance élevé entre deux signaux d'activation décalés d'un pas de temps est un phénomène relativement rare. Une majorité de neurones (neurones saturés et muets) émettent un signal de très faible amplitude. Seuls les covariances entre des neurones dynamiques peuvent atteindre des valeurs plus importantes, à la condition que leurs signaux soient corrélés en 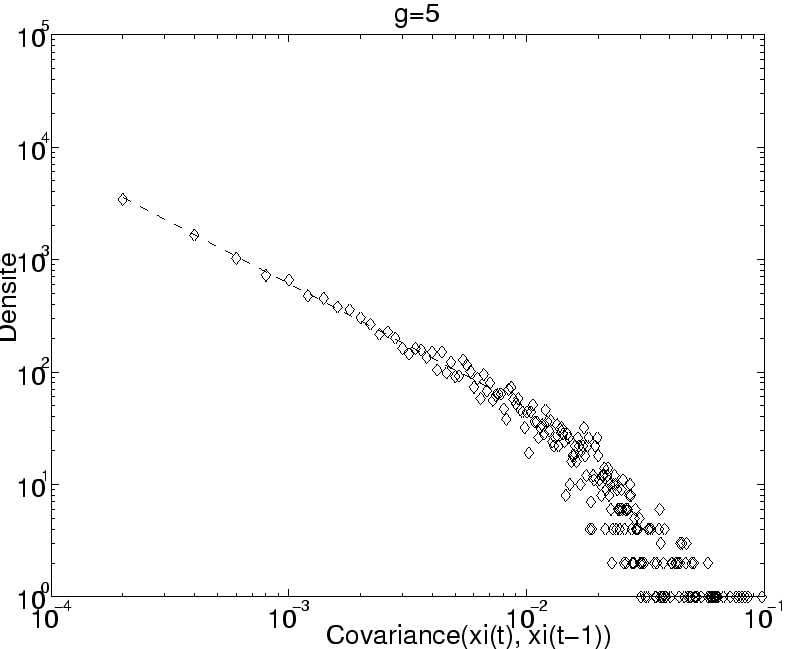$(t,t-1)$ (ou anticorrélés).

Cette distribution en loi de puissance se maintient pour tout réseau sur les différents régimes dynamiques. L'exposant $b$ tend à diminuer au cours de la route vers le chaos, ce qui indique une homogénéisation progressive des activités dynamiques individuelles.