




suivant: Comportement statistique de la
monter: Covariance des activations
précédent: Covariance des activations
Table des matières
Index
Règle de covariance
Les limites des règles d'apprentissage qui reposent sur les caractéristiques statiques des activations ont été à peu près cernées.
En particulier, il est apparu sur la première règle étudiée (4.1), qui est fondée sur un produit entre les activations effectives, que le terme constant 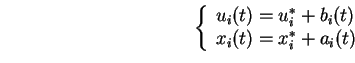 intervient de façon décisive dans le changement synaptique.
De manière globale, la règle tend à renforcer l'influence des neurones dont l'activation est la plus forte en moyenne, c'est à dire les neurones saturés.
Sachant que les neurones saturés produisent un signal d'activation d'amplitude très faible, on augmente l'influence des neurones qui sont les moins représentatifs de la dynamique.
intervient de façon décisive dans le changement synaptique.
De manière globale, la règle tend à renforcer l'influence des neurones dont l'activation est la plus forte en moyenne, c'est à dire les neurones saturés.
Sachant que les neurones saturés produisent un signal d'activation d'amplitude très faible, on augmente l'influence des neurones qui sont les moins représentatifs de la dynamique.
Il paraît dès lors logique de mettre en place une règle qui gomme les aspects statiques du signal d'activation, c'est à dire qui néglige autant que possible sa partie constante.
Lorsque l'on souhaite renforcer l'intensité des signaux propagés, la quantité qui nous intéresse est la partie dynamique du signal d'activation
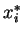 .
.
La mise en 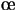 uvre de cette nouvelle règle nécessite d'utiliser l'estimation instantanée de l'activation moyenne
uvre de cette nouvelle règle nécessite d'utiliser l'estimation instantanée de l'activation moyenne
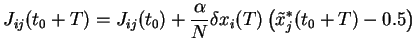 .
Cette variable conserve à tout instant une mémoire de l'activation moyenne , remise à jour à chaque pas de temps selon le paramètre d'habituation
.
Cette variable conserve à tout instant une mémoire de l'activation moyenne , remise à jour à chaque pas de temps selon le paramètre d'habituation 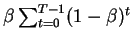 (voir page
(voir page ![[*]](/usr/share/latex2html/icons/crossref.png) ).
On accède ainsi à tout instant
).
On accède ainsi à tout instant 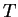 à une estimation de l'activité dynamique
à une estimation de l'activité dynamique
Et (en régime stationnaire) on a :
Pour 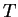 grand :
grand :
Comme précédemment, une valeur de 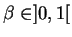 proche de zéro améliore l'estimation sur l'activité dynamique.
La valeur opérationnelle
proche de zéro améliore l'estimation sur l'activité dynamique.
La valeur opérationnelle 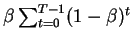 nécessite un temps de convergence d'environ 60 pas de temps.
nécessite un temps de convergence d'environ 60 pas de temps.
Le mécanisme d'adaptation synaptique proposé ici reste fondamentalement un mécanisme Hebbien.
Le but de la nouvelle règle d'apprentissage est de modifier les liens synaptiques 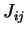 selon les caractéristiques de l'activité dynamique
selon les caractéristiques de l'activité dynamique 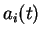 exclusivement.
Dans notre système, le principe général de Hebb doit subir quelques adaptations :
exclusivement.
Dans notre système, le principe général de Hebb doit subir quelques adaptations :
- Dans le modèle biologique, l'activation d'un neurone est un événement rare. Dans notre modèle, comme on l'a vu, les évènements rares (et donc ``chargés de sens'') sont les activités dynamiques de grande amplitude.
- Notre modèle est à états continus. La co-occurrence de spikes peut être fonctionnellement remplacée par la covariance, qui prend en compte l'amplitude des signaux afférents et récepteurs.
Il est possible d'avoir une covariance négative.
- Contrairement au modèle biologique, où inhibiteurs et excitateurs sont séparés, tout neurone envoie à la fois des connexions inhibitrices et excitatrices.
L'équivalent du renforcement d'un lien excitateur doit être l'affaiblissement (en valeur absolue) d'un lien inhibiteur.
Inversement, l'équivalent de l'affaiblissement d'un lien excitateur doit être le renforcement (en valeur absolue) d'un lien inhibiteur.
- Le délai biologique
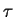 est le délai 1 qui correspond à la mise à jour synchrone des états des neurones.
est le délai 1 qui correspond à la mise à jour synchrone des états des neurones.
On traduit le mécanisme de Hebb par la dynamique sur les poids (4.4),
fondée sur le produit des activités dynamiques entre l'activité des neurones émetteurs au temps 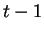 et l'activité des neurones récepteurs au temps
et l'activité des neurones récepteurs au temps  .
Il est important de bien insister sur le rôle majeur que joue à présent le délai de transmission
.
Il est important de bien insister sur le rôle majeur que joue à présent le délai de transmission 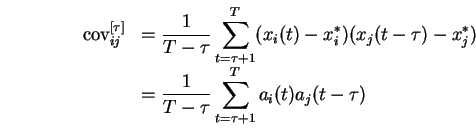 .
Le renforcement des liens se fonde sur les caractéristiques des signaux antérieurs d'un pas de temps au signal actuel.
Les règles analogues présentes dans la littérature [55] ne prennent pas en compte ce délai temporel.
[59] montre l'importance de la prise en compte du délai de transmission pour des systèmes visant à apprendre des motifs spatio-temporels.
.
Le renforcement des liens se fonde sur les caractéristiques des signaux antérieurs d'un pas de temps au signal actuel.
Les règles analogues présentes dans la littérature [55] ne prennent pas en compte ce délai temporel.
[59] montre l'importance de la prise en compte du délai de transmission pour des systèmes visant à apprendre des motifs spatio-temporels.
À chaque pas de temps, chaque neurone  modifie ses poids afférents
modifie ses poids afférents 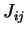 selon la règle :
selon la règle :
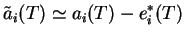 |
(4.4) |
La notation 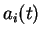 qui apparaît dans la règle d'apprentissage, désigne en fait
qui apparaît dans la règle d'apprentissage, désigne en fait
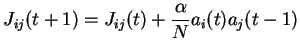 dans la mise en
dans la mise en 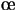 uvre numérique, avec pour valeur opérationnelle
uvre numérique, avec pour valeur opérationnelle 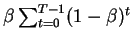 .
.
- Si le produit
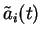 , la valeur du poids augmente.
, la valeur du poids augmente.
- Si le poids est excitateur, il est renforcé et devient plus excitateur.
- Si le poids est inhibiteur, il est affaibli et devient moins inhibiteur.
- Si le produit
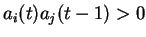 , la valeur du poids diminue.
, la valeur du poids diminue.
- Si le poids est excitateur, il est est affaibli et devient moins excitateur.
- Si le poids est inhibiteur, il est renforcé et devient plus inhibiteur
(il propage l'opposé du signal afférent). Ainsi, si
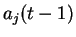 est opposé à
est opposé à 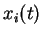 ,
,
 est de même signe que
est de même signe que 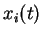 , et cette co-activation est renforcée.
Moins par moins égale plus.
, et cette co-activation est renforcée.
Moins par moins égale plus.
On voit que les liens ``excitateur'' et ``inhibiteur'' jouent des rôles symétriques, ce qui n'est pas le cas des neurones biologiques.
Si un des deux neurones est saturé ou silencieux, le produit
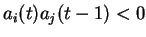 est proche de zéro, et par conséquent le poids change très peu.
L'essentiel des modifications de poids s'effectue sur les liaisons entre neurones actifs.
est proche de zéro, et par conséquent le poids change très peu.
L'essentiel des modifications de poids s'effectue sur les liaisons entre neurones actifs.
La règle que nous avons mise en place repose fondamentalement, comme nous allons le voir, sur une estimation de la covariance effective entre les signaux d'activation afférents et efférents.
Au prix d'une hypothèse de stationnarité du processus d'apprentissage, on peut montrer que les modifications synaptiques inscrites par la règle sont en effet proportionnelles à cette covariance.
Ainsi, si l'apprentissage est effectué entre 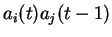 et
et 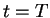 , et si dans ce cas on prend une valeur d'
, et si dans ce cas on prend une valeur d'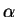 suffisamment petite pour que l'hypothèse de stationnarité soit correctement approchée, alors :
suffisamment petite pour que l'hypothèse de stationnarité soit correctement approchée, alors :
Dans le cas général, l'influence de la covariance des activations sur le renforcement des poids reste, comme nous le verrons plus loin, tout à fait fondamentale.
La règle renforce les liens propageant des signaux corrélés à 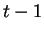 au signal du neurone au temps
au signal du neurone au temps  , ce qui revient à renforcer les liens entre les différentes étapes du circuit d'activation.
, ce qui revient à renforcer les liens entre les différentes étapes du circuit d'activation.
Avant l'étude des effets de l'apprentissage sur la dynamique, la section suivante propose un aperçu de la répartition de ces covariances sur nos réseaux.





suivant: Comportement statistique de la
monter: Covariance des activations
précédent: Covariance des activations
Table des matières
Index
Dauce Emmanuel
2003-05-07
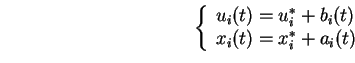 intervient de façon décisive dans le changement synaptique.
De manière globale, la règle tend à renforcer l'influence des neurones dont l'activation est la plus forte en moyenne, c'est à dire les neurones saturés.
Sachant que les neurones saturés produisent un signal d'activation d'amplitude très faible, on augmente l'influence des neurones qui sont les moins représentatifs de la dynamique.
intervient de façon décisive dans le changement synaptique.
De manière globale, la règle tend à renforcer l'influence des neurones dont l'activation est la plus forte en moyenne, c'est à dire les neurones saturés.
Sachant que les neurones saturés produisent un signal d'activation d'amplitude très faible, on augmente l'influence des neurones qui sont les moins représentatifs de la dynamique.
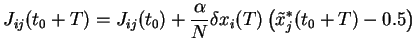 .
Cette variable conserve à tout instant une mémoire de l'activation moyenne , remise à jour à chaque pas de temps selon le paramètre d'habituation
.
Cette variable conserve à tout instant une mémoire de l'activation moyenne , remise à jour à chaque pas de temps selon le paramètre d'habituation 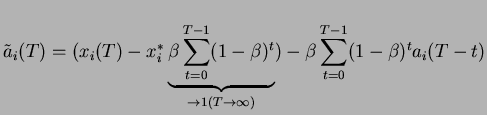
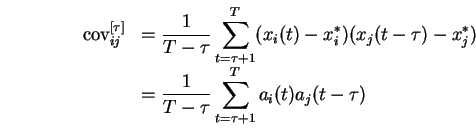 .
Le renforcement des liens se fonde sur les caractéristiques des signaux antérieurs d'un pas de temps au signal actuel.
Les règles analogues présentes dans la littérature [
.
Le renforcement des liens se fonde sur les caractéristiques des signaux antérieurs d'un pas de temps au signal actuel.
Les règles analogues présentes dans la littérature [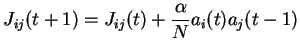 dans la mise en
dans la mise en