Cette règle d'apprentissage et ses résultats ont été présentés à ICANN'98 [96].
L'idée qui sous tend la mise en place de cette nouvelle règle d'apprentissage est le principe d'habituation, selon lequel un neurone favorise ce qui est nouveau dans son environnement, et néglige ce qui ne change pas. Ce principe est bien connu dans le cas des neurones biologiques [97].
L'idée de départ est que chaque neurone possède une estimation instantanée de la valeur de l'activation moyenne de chacun de ses afférents
![]() .
Cette estimation est remise à jour à chaque pas de temps selon :
.
Cette estimation est remise à jour à chaque pas de temps selon :
où
![$ \beta \in ]0,1[$](img873.png) est le paramètre qui règle l'habituation (
est le paramètre qui règle l'habituation (![]() est un paramètre arbitraire indépendant des autres paramètres).
est un paramètre arbitraire indépendant des autres paramètres).
Si on considère un signal d'activation
![]() , on a :
, on a :
Dans cette formule, ![]() peut être vu comme un terme de normalisation, dans la mesure où
peut être vu comme un terme de normalisation, dans la mesure où
 tend vers
tend vers ![]() quand
quand
![]() .
On voit alors que
.
On voit alors que
![]() nous donne, au même titre que la moyenne empirique, une estimation de l'activation fondée sur la totalité des valeurs du signal.
Néanmoins, du fait de la pondération sur le temps, seuls les états les plus proches temporellement de
nous donne, au même titre que la moyenne empirique, une estimation de l'activation fondée sur la totalité des valeurs du signal.
Néanmoins, du fait de la pondération sur le temps, seuls les états les plus proches temporellement de ![]() sont effectivement pris en compte pour le calcul de cette moyenne.
sont effectivement pris en compte pour le calcul de cette moyenne.
Si le signal est stationnaire, on peut estimer l'écart par rapport à sa moyenne effective 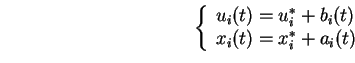 (sachant que
(sachant que
![]() ) comme suit :
) comme suit :

Si ![]() vaut 1, le terme d'écart correspond à l'activité dynamique
vaut 1, le terme d'écart correspond à l'activité dynamique ![]() du neurone au temps
du neurone au temps ![]() .
Pour des valeurs élevées de
.
Pour des valeurs élevées de ![]() , l'estimation tend à reproduire (de manière affaiblie) les fluctuations temporelles du signal d'activation.
Plus
, l'estimation tend à reproduire (de manière affaiblie) les fluctuations temporelles du signal d'activation.
Plus ![]() se rapproche de zéro, plus le terme d'écart se rapproche également de zéro, en tant qu'estimation de la moyenne du signal centré
se rapproche de zéro, plus le terme d'écart se rapproche également de zéro, en tant qu'estimation de la moyenne du signal centré ![]() .
L'estimation de
.
L'estimation de 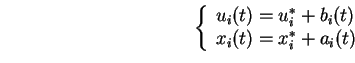 est d'autant meilleure que
est d'autant meilleure que ![]() est petit, dans la mesure où les activations anciennes sont mieux prises en compte.
est petit, dans la mesure où les activations anciennes sont mieux prises en compte.
À l'inverse, on peut remarquer que plus ![]() est petit, plus il faut que
est petit, plus il faut que ![]() soit élevé pour que l'autre terme d'écart
soit élevé pour que l'autre terme d'écart
 soit proche de 1.
Le comportement de ce terme d'écart avec
soit proche de 1.
Le comportement de ce terme d'écart avec ![]() permet d'estimer le temps de convergence.
permet d'estimer le temps de convergence.
Une valeur opérationnelle de ![]() , permettant une bonne estimation de l'activation moyenne en entrée est
, permettant une bonne estimation de l'activation moyenne en entrée est ![]() .
Elle nécessite que
.
Elle nécessite que ![]() pour que l'écart du au temps de convergence soit inférieur à
pour que l'écart du au temps de convergence soit inférieur à ![]() .
.
Lorsque l'on itère la dynamique spontanée du réseau, si à un instant ![]() , on présente un motif statique, le système tend à se réorganiser.
La dynamique converge vers son nouvel attracteur, et, au cours de ce temps de relaxation la dynamique est non stationnaire.
En particulier, pour chaque neurone, l'activation moyenne
, on présente un motif statique, le système tend à se réorganiser.
La dynamique converge vers son nouvel attracteur, et, au cours de ce temps de relaxation la dynamique est non stationnaire.
En particulier, pour chaque neurone, l'activation moyenne
![]() est amenée à évoluer vers une nouvelle valeur stationnaire.
La différence entre l'activation moyenne qui précède la présentation du motif et celle qui suit la présentation du motif constitue le différentiel d'activation
est amenée à évoluer vers une nouvelle valeur stationnaire.
La différence entre l'activation moyenne qui précède la présentation du motif et celle qui suit la présentation du motif constitue le différentiel d'activation
![]() .
En pratique, si
.
En pratique, si ![]() est le temps où le motif est présenté, et
est le temps où le motif est présenté, et ![]() le temps de relaxation4.1, on a :
le temps de relaxation4.1, on a :
Les différentiels d'activation les plus élevés correspondent aux neurones qui sont le plus fortement influencés par la présentation du motif.
Si on n'autorise la modification des poids que pour les neurones sources dont le différentiel d'activation est supérieur à un certain seuil ![]() , on est sûr de sélectionner les neurones qui sont le plus spécifiquement liés au motif présenté.
Pour les simulations, on a pris en général
, on est sûr de sélectionner les neurones qui sont le plus spécifiquement liés au motif présenté.
Pour les simulations, on a pris en général ![]() , ce qui permet de sélectionner environ 5%
des neurones, pour un motif d'écart-type
, ce qui permet de sélectionner environ 5%
des neurones, pour un motif d'écart-type
![]() .
.
Une fois la sélection opérée, la variation des poids repose sur un produit entre l'activation moyenne du neurone source (moins le seuil) et le différentiel d'activation du neurone cible.
Chaque fois que l'on veut itérer la règle d'apprentissage, il faut laisser relaxer la dynamique spontanée, présenter le motif à apprendre, laisser relaxer la dynamique contrainte, et effectuer la modification des poids synaptiques.
En prenant des temps de relaxation ![]() , il faut donc itérer 200 pas de la dynamique rapide par pas d'apprentissage.
, il faut donc itérer 200 pas de la dynamique rapide par pas d'apprentissage.
Sous forme algorithmique :
Pour tout, pour tout
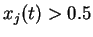
Sialors
Sinon on ne modifie pas les poids.
Avec ce type de règle, le neurone renforce la corrélation entre son différentiel d'activation et la valeur de l'activation moyenne des neurones les plus spécifiquement liés au motif (ces neurones spécifiques sont ceux qui sont sélectionnés par la condition
![]() ).
Par la suite, chaque fois que le même motif sera présenté, l'activation des mêmes neurones spécifiques tendra à provoquer un différentiel d'activation plus important sur tous les neurones, donc à translater les potentiels moyens des neurones vers des valeurs plus excentrées en moyenne, et donc à favoriser un affaiblissemnent de la dynamique.
).
Par la suite, chaque fois que le même motif sera présenté, l'activation des mêmes neurones spécifiques tendra à provoquer un différentiel d'activation plus important sur tous les neurones, donc à translater les potentiels moyens des neurones vers des valeurs plus excentrées en moyenne, et donc à favoriser un affaiblissemnent de la dynamique.
Avec ce type de règle d'apprentissage, qui prend en compte une mémoire de l'état moyen du réseau, on arrive à diviser par 10 en moyenne les effets de bord de la dynamique d'apprentissage. Autrement dit, en apprenant 10 motifs, on aura en moyenne les mêmes effets de bord que lorsque l'on en apprenait 1 pour la règle précédente. En fin de compte, l'efficacité de ce type de règle repose sur une capacité à sélectionner quelques neurones et quelques liens qui sont les plus spécifiques de la dynamique contrainte, et à translater les potentiels des bons neurones pour éteindre la dynamique.
Un des points qui illustre le plus nettement le fait que l'on atteint nécessairement une capacité limite se fonde sur l'observation des réductions de dynamique obtenues par apprentissage de motifs binaires, tels que 5% des neurones du réseau soient excités par ce motif. Outre les réductions de dynamique spécifiquement associées aux motifs appris, on constate en effet que des motifs qui sont des combinaisons des motifs appris tendent également à réduire la dynamique. Cette réduction est également observée pour des versions bruitées (ajout et retrait au hasard de certaines valeurs binaires) des motifs appris. Plus le nombre de motifs appris est grand, plus le nombre de combinaisons possibles est élevé et plus il y a de chance qu'un motif quelconque soit proche d'une combinaison de plusieurs motifs appris. Dans ces conditions, on comprend mieux la perte de spécificité liée à l'apprentissage d'un grand nombre de motifs.
En conclusion, les deux règles présentées fondent les changements synaptiques sur les caractéristiques statiques de la dynamique, c'est à dire sur des niveaux moyens d'activation. Ceci a pour conséquence la réduction systématique de l'écart-type et de la complexité de la dynamique au cours de l'apprentissage. On comprend dès lors que l'effet d'un apprentissage poussé trop loin provoque systématiquement un effondrement généralisé de la dynamique. C'est pour cette raison que l'on va maintenant s'intéresser à un autre type de règle, qui ne se fonde que sur les caractéristiques dynamiques de l'activation des neurones, et tend au contraire à renforcer l'activité dynamique des réseaux.