




suivant: Différentiels d'activation
monter: Historique
précédent: Historique
Table des matières
Index
La règle initiale
La première règle a été présentée dans la thèse de Mathias Quoy [95].
La règle de Hebb, qui porte sur des liens excitateurs, dit que le lien synaptique est renforcé lorsqu'un pic d'activation sur le neurone afférent est suivi, dans un intervalle de temps 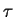 , d'un pic d'activation sur le neurone récepteur.
Dans le cas où l'activation du neurone afférent n'est pas suivie par une activation du neurone récepteur, le lien est légèrement diminué.
, d'un pic d'activation sur le neurone récepteur.
Dans le cas où l'activation du neurone afférent n'est pas suivie par une activation du neurone récepteur, le lien est légèrement diminué.
La première règle proposée sur notre modèle, d'inspiration hebbienne, repose par ailleurs sur deux principes forts :
- La dynamique sur les poids repose sur un produit des activations, avec un délai d'un pas de temps entre le neurone source et le neurone cible qui représente le délai de transmission sur l'axone.
- La dynamique d'apprentissage est adiabatique. C'est une dynamique lente par rapport à la dynamique sur les activations.
À chaque modification des poids, on a une centaine de pas de relaxation permettant à la dynamique de rejoindre son nouvel attracteur.
On fixe par avance le temps de relaxation :
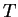 .
.
Trois contraintes complètent cette règle :
- on exige une activation minimale (
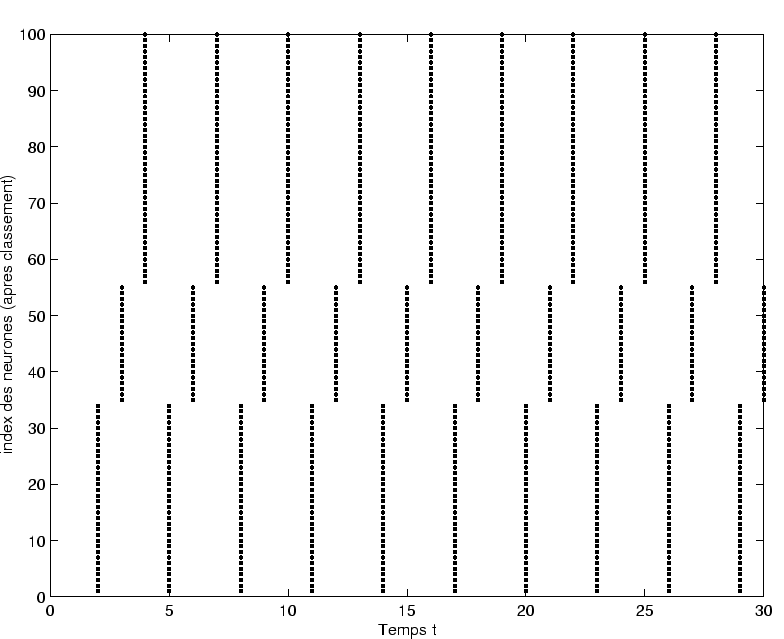 ) du neurone source pour engendrer une modification du lien, ce qui revient à dire : lorsque le neurone source est inactif, il ne se passe rien.
) du neurone source pour engendrer une modification du lien, ce qui revient à dire : lorsque le neurone source est inactif, il ne se passe rien.
- pour des raisons de plausibilité biologique, un poids ne peut pas changer de signe i.e. : un lien inhibiteur ne peut pas devenir excitateur.
- les neurones ne possèdent pas de lien propre, soit
 ; la règle n'agit donc pas sur ce lien.
; la règle n'agit donc pas sur ce lien.
Ce qui donne, sous forme algorithmique :
(Tous les 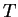 pas de temps, pour tout
pas de temps, pour tout  , pour tout
, pour tout 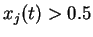 )
)
Si
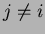 alors
alors
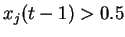 |
(4.1) |
Sinon on ne modifie pas les poids.
Si l'activation du neurone cible est 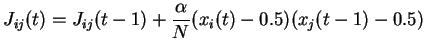 , le poids est augmenté.
Si l'activation du neurone cible est
, le poids est augmenté.
Si l'activation du neurone cible est 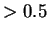 , le poids est diminué.
Le paramètre qui règle la force de l'apprentissage est
, le poids est diminué.
Le paramètre qui règle la force de l'apprentissage est 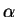 .
On prend souvent des valeurs d'
.
On prend souvent des valeurs d'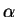 comprises entre 0.01 et 0.1.
La normalisation d'
comprises entre 0.01 et 0.1.
La normalisation d'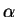 en
en 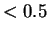 permet d'avoir un impact équivalent en moyenne sur le champ local du neurone, quelle que soit la taille du réseau.
En contrepartie, plus la taille est grande, plus l'effet de l'apprentissage sur un lien particulier est faible.
permet d'avoir un impact équivalent en moyenne sur le champ local du neurone, quelle que soit la taille du réseau.
En contrepartie, plus la taille est grande, plus l'effet de l'apprentissage sur un lien particulier est faible.
Une expérience d'apprentissage se déroule typiquement comme suit : après initialisation des poids 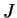 et du motif
et du motif 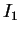 , on itère les transitoires jusqu'à atteindre la dynamique stationnaire.
Chaque modification des poids est suivie de
, on itère les transitoires jusqu'à atteindre la dynamique stationnaire.
Chaque modification des poids est suivie de 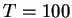 transitoires, et l'opération est répétée jusqu'à l'obtention d'une dynamique périodique (voir premier point ci-dessous).
La nouvelle matrice des poids
transitoires, et l'opération est répétée jusqu'à l'obtention d'une dynamique périodique (voir premier point ci-dessous).
La nouvelle matrice des poids 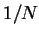 sert ensuite de base aux différents tests sur les caractéristiques de cet apprentissage.
sert ensuite de base aux différents tests sur les caractéristiques de cet apprentissage.
Cette règle a permis de mettre en évidence les résultats suivants :
- L'effet principal de la règle d'apprentisage est de provoquer une réduction continue de la complexité de l'activité dynamique.
Ainsi, à
 fixé, si la dynamique de départ est de type chaotique, on observe au cours de l'apprentissage une route inverse qui va du chaos vers le point fixe en passant par des cycles limites.
Ce résultat dynamique spectaculaire est obtenu en modifiant très faiblement les poids synaptiques.
Dans le cadre de nos expériences, 10 à 20 modifications synaptiques, avec
fixé, si la dynamique de départ est de type chaotique, on observe au cours de l'apprentissage une route inverse qui va du chaos vers le point fixe en passant par des cycles limites.
Ce résultat dynamique spectaculaire est obtenu en modifiant très faiblement les poids synaptiques.
Dans le cadre de nos expériences, 10 à 20 modifications synaptiques, avec
 , suffisent pour atteindre un régime de type cycle limite.
, suffisent pour atteindre un régime de type cycle limite.
- La modification des poids synaptiques est de très faible amplitude.
On prend conscience que nos régimes dynamiques sont fragiles.
Toute l'organisation dynamique spontanée peut être détruite par quelques changements très ciblés des poids.
- Le changement dynamique est spécifique, dans la mesure où il s'applique à la dynamique issue de l'association entre les poids
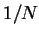 et le motif appris
et le motif appris 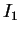 .
En particulier, la présentation d'un autre motif
.
En particulier, la présentation d'un autre motif 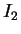 n'a pas d'effet spécifique sur la dynamique.
Cette propriété nous permet d'associer ce comportement dynamique cyclique à ce motif.
Schématiquement, ce comportement est comparable à celui observé par Freeman sur le bulbe olfactif du lapin.
n'a pas d'effet spécifique sur la dynamique.
Cette propriété nous permet d'associer ce comportement dynamique cyclique à ce motif.
Schématiquement, ce comportement est comparable à celui observé par Freeman sur le bulbe olfactif du lapin.
Ces résultats présentés dans la thèse de Mathias Quoy ont pu être approfondis grâce à un apport personnel portant sur la répartition de l'activité dynamique des neurones (voir section 3.1.1).
Tous ces résultats ont donné lieu à publication [82]
L'évolution de ces répartitions en cours d'apprentissage a permis de mieux comprendre les mécanismes mis en jeu :
- L'apprentissage agit essentiellement sur la configuration spatiale (activations moyennes) associée au motif
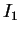 .
En particulier, les neurones dits ``saturés'', dont l'activation est proche de 1 et l'activité dynamique faible, ont une influence prépondérante.
En effet, les liens en provenance de ces neurones sont systématiquement renforcés.
.
En particulier, les neurones dits ``saturés'', dont l'activation est proche de 1 et l'activité dynamique faible, ont une influence prépondérante.
En effet, les liens en provenance de ces neurones sont systématiquement renforcés.
- La règle provoque en moyenne une translation des potentiels moyens des neurones vers des valeurs excentrées.
Or, plus le potentiel moyen est excentré, moins le neurone est actif.
On a donc un appauvrissement en neurones actifs, qui provoque l'effondrement dynamique observé.
Une conséquence importante est que l'on perd la distribution gaussienne des potentiels, qui constitue le socle des équations de champ moyen.
On sort donc du cadre de la théorie du champ moyen dès que l'on met en
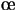 uvre la règle d'apprentissage.
uvre la règle d'apprentissage.
- La modification de l'entrée statique (motif
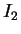 ) provoque une nouvelle configuration spatiale, et en particulier une redistribution des neurones saturés.
La dynamique associée à
) provoque une nouvelle configuration spatiale, et en particulier une redistribution des neurones saturés.
La dynamique associée à 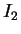 est cependant influencée de façon marginale par les modifications synaptiques.
On peut parler d'effet de bord de l'apprentissage.
Cet effet de bord se mesure à la proportion de neurones saturés communs entre la dynamique associée à
est cependant influencée de façon marginale par les modifications synaptiques.
On peut parler d'effet de bord de l'apprentissage.
Cet effet de bord se mesure à la proportion de neurones saturés communs entre la dynamique associée à 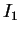 et la dynamique associée à
et la dynamique associée à 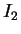 .
.
Le résultat principal est donc que l'apprentissage a des effets de bord.
Par malheur, ces effets de bord deviennent prépondérants lorsque l'on veut apprendre plusieurs motifs.
Chaque nouvel apprentissage sur un motif 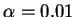 déplace les potentiels d'une partie des neurones vers des valeurs excentrées, ce qui tend à effondrer la dynamique pour tout motif
déplace les potentiels d'une partie des neurones vers des valeurs excentrées, ce qui tend à effondrer la dynamique pour tout motif 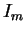 tel que l'entretien de cette dynamique reposait initialement sur certains des neurones déplacés.
Plus on apprend de motifs, plus l'ensemble des neurones ainsi déplacés est important, et plus il est probable que la présentation d'un motif quelconque
tel que l'entretien de cette dynamique reposait initialement sur certains des neurones déplacés.
Plus on apprend de motifs, plus l'ensemble des neurones ainsi déplacés est important, et plus il est probable que la présentation d'un motif quelconque 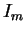 effondre la dynamique du réseau.
On perd ainsi progressivement la propriété de spécificité dynamique associée aux motifs appris.
La capacité maximale du réseau est en fait rapidement atteinte.
effondre la dynamique du réseau.
On perd ainsi progressivement la propriété de spécificité dynamique associée aux motifs appris.
La capacité maximale du réseau est en fait rapidement atteinte.
Cette capacité dépend en grande partie des choix des paramètres initiaux.
Des mesures précises ont été effectuées pour les paramètres suivants, et sont présentées dans [82] :
- on choisit un paramètre de gain élevé (
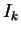 ), de manière à ce que la dynamique spontanée développée dans les réseaux soit éloignée de la frontière du chaos, et donc peu sensible aux effets de bord produits par l'apprentissage.
), de manière à ce que la dynamique spontanée développée dans les réseaux soit éloignée de la frontière du chaos, et donc peu sensible aux effets de bord produits par l'apprentissage.
- on prend des motifs aléatoires statiques centrés dont l'écart-type est élevé (
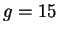 ), afin que les changements de motifs tendent à redistribuer fortement la configuration spatiale des activations.
), afin que les changements de motifs tendent à redistribuer fortement la configuration spatiale des activations.
- La taille est relativement élevée
 .
.
Dans ces conditions, les effets de bord sont de l'ordre de 12 à 16%
par motif appris, c'est à dire qu'après apprentissage, 12 à 16%
des motifs quelconques présentés induisent une réduction dynamique non souhaitée.
On voit donc dans ces conditions que la limitation en termes de capacité est sérieuse.
À l'issue de l'étude sur cette première règle d'apprentissage, deux constatations peuvent être faites :
- La principale limitation de la règle vient du renforcement de neurones non-spécifiques.
Il faut donc opérer une sélection plus importante sur le choix des poids à modifier afin de limiter les effets de bord.
- L'essentiel des modifications synaptiques provient des neurones saturés à activité dynamique faible.
Dans les faits, la règle prend essentiellement en compte l'activation moyenne des neurones, et non la composante temporelle du signal d'activation.
En conséquence, les délais présents dans la règle d'apprentissage n'ont aucun rôle en pratique.
Il faut donc renforcer la prise en compte de cette information temporelle.
C'est pour pallier à cette capacité faible qu'on a cherché à mettre en place des règles d'apprentissage moins coûteuses.
Ces considérations ont abouti à la mise en 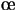 uvre de deux nouveaux types de règles d'apprentissage, qui ont été explorés successivement :
uvre de deux nouveaux types de règles d'apprentissage, qui ont été explorés successivement :
- Dans un premier temps, on a cherché à mettre en place des règles d'apprentissage fondées sur des différentiels d'activation, c'est à dire qui renforcent les neurones dont l'activation moyenne est la plus fortement modifié suite à la présentation d'un motif.
Le principe de la dynamique d'apprentissage adiabatique est conservé, et les délais de transmission sont abandonnés.
- Dans un deuxième temps, on a cherché à mettre en place des règles d'apprentissage qui ne prennent en compte que les caractéristiques dynamiques des signaux émis par les neurones.
Dans ce cas, la prise en compte du délai de transmission devient prépondérante, mais on abandonne par contre la dynamique adiabatique.
C'est la deuxième voie qui a été la plus fructueuse, et qui sera développée en détail dans la suite de ce rapport, mais voyons dans un premier temps les résultats obtenus pour le premier type de règles d'apprentissage, et ce qu'ils apportent.





suivant: Différentiels d'activation
monter: Historique
précédent: Historique
Table des matières
Index
Dauce Emmanuel
2003-05-07
![]() , d'un pic d'activation sur le neurone récepteur.
Dans le cas où l'activation du neurone afférent n'est pas suivie par une activation du neurone récepteur, le lien est légèrement diminué.
, d'un pic d'activation sur le neurone récepteur.
Dans le cas où l'activation du neurone afférent n'est pas suivie par une activation du neurone récepteur, le lien est légèrement diminué.
 ) du neurone source pour engendrer une modification du lien, ce qui revient à dire : lorsque le neurone source est inactif, il ne se passe rien.
) du neurone source pour engendrer une modification du lien, ce qui revient à dire : lorsque le neurone source est inactif, il ne se passe rien.
pas de temps, pour tout
, pour tout
)
alors
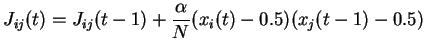 , le poids est augmenté.
Si l'activation du neurone cible est
, le poids est augmenté.
Si l'activation du neurone cible est ![]() , le poids est diminué.
Le paramètre qui règle la force de l'apprentissage est
, le poids est diminué.
Le paramètre qui règle la force de l'apprentissage est ![]() .
On prend souvent des valeurs d'
.
On prend souvent des valeurs d'![]() comprises entre 0.01 et 0.1.
La normalisation d'
comprises entre 0.01 et 0.1.
La normalisation d'![]() en
en ![]() permet d'avoir un impact équivalent en moyenne sur le champ local du neurone, quelle que soit la taille du réseau.
En contrepartie, plus la taille est grande, plus l'effet de l'apprentissage sur un lien particulier est faible.
permet d'avoir un impact équivalent en moyenne sur le champ local du neurone, quelle que soit la taille du réseau.
En contrepartie, plus la taille est grande, plus l'effet de l'apprentissage sur un lien particulier est faible.
![]() et du motif
et du motif ![]() , on itère les transitoires jusqu'à atteindre la dynamique stationnaire.
Chaque modification des poids est suivie de
, on itère les transitoires jusqu'à atteindre la dynamique stationnaire.
Chaque modification des poids est suivie de ![]() transitoires, et l'opération est répétée jusqu'à l'obtention d'une dynamique périodique (voir premier point ci-dessous).
La nouvelle matrice des poids
transitoires, et l'opération est répétée jusqu'à l'obtention d'une dynamique périodique (voir premier point ci-dessous).
La nouvelle matrice des poids ![]() sert ensuite de base aux différents tests sur les caractéristiques de cet apprentissage.
sert ensuite de base aux différents tests sur les caractéristiques de cet apprentissage.
![]() déplace les potentiels d'une partie des neurones vers des valeurs excentrées, ce qui tend à effondrer la dynamique pour tout motif
déplace les potentiels d'une partie des neurones vers des valeurs excentrées, ce qui tend à effondrer la dynamique pour tout motif ![]() tel que l'entretien de cette dynamique reposait initialement sur certains des neurones déplacés.
Plus on apprend de motifs, plus l'ensemble des neurones ainsi déplacés est important, et plus il est probable que la présentation d'un motif quelconque
tel que l'entretien de cette dynamique reposait initialement sur certains des neurones déplacés.
Plus on apprend de motifs, plus l'ensemble des neurones ainsi déplacés est important, et plus il est probable que la présentation d'un motif quelconque ![]() effondre la dynamique du réseau.
On perd ainsi progressivement la propriété de spécificité dynamique associée aux motifs appris.
La capacité maximale du réseau est en fait rapidement atteinte.
effondre la dynamique du réseau.
On perd ainsi progressivement la propriété de spécificité dynamique associée aux motifs appris.
La capacité maximale du réseau est en fait rapidement atteinte.
![]() uvre de deux nouveaux types de règles d'apprentissage, qui ont été explorés successivement :
uvre de deux nouveaux types de règles d'apprentissage, qui ont été explorés successivement :