Sur un réseau de taille ![]() , la dynamique spontanée est itérée jusqu'à ce que la dynamique soit estimée suffisamment proche de la stationnarité.
Le temps
, la dynamique spontanée est itérée jusqu'à ce que la dynamique soit estimée suffisamment proche de la stationnarité.
Le temps ![]() marque cette entrée en dynamique stationnaire.
La valeur de
marque cette entrée en dynamique stationnaire.
La valeur de ![]() a été choisie afin que le système soit en régime pseudo-périodique.
De
a été choisie afin que le système soit en régime pseudo-périodique.
De ![]() à
à ![]() , la dynamique d'apprentissage est itérée, avec
, la dynamique d'apprentissage est itérée, avec
![]() .
La figure 4.2 présente l'évolution du signal moyen
.
La figure 4.2 présente l'évolution du signal moyen ![]() , avec
, avec ![]() . L'apprentissage est arrêté arbitrairement après
. L'apprentissage est arrêté arbitrairement après ![]() pas de temps (deux valeurs de
pas de temps (deux valeurs de ![]() sont utilisées :
sont utilisées : ![]() et
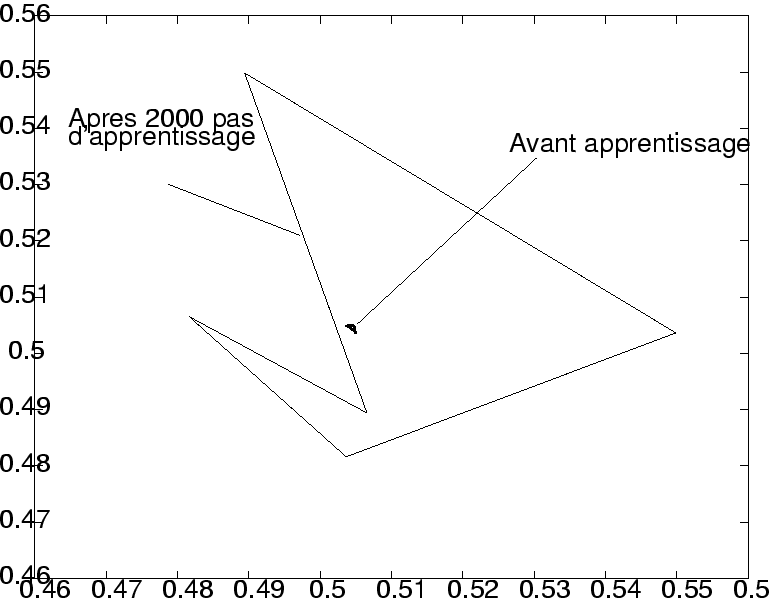
et ![]() ). La dynamique spontanée est itérée après apprentissage sur 1000 pas de temps supplémentaires (avec la nouvelle matrice de poids).
). La dynamique spontanée est itérée après apprentissage sur 1000 pas de temps supplémentaires (avec la nouvelle matrice de poids).
![\includegraphics[]{app_cycle_1000_attr.eps}](img916.png)
![\includegraphics[]{app_cycle_2000.eps}](img917.png)
![\includegraphics[]{app_cycle_2000_attr.eps}](img918.png)
|
Lorsque la dynamique initiale est un cycle limite d'amplitude faible, on constate d'emblée que la dynamique d'apprentissage tend à augmenter l'amplitude du signal moyen.
Cet effet sur l'observable global correspond localement à une augmentation de l'amplitude moyenne des signaux individuels.
En effet, si le signal d'activation ![]() est corrélé au signal d'activation
est corrélé au signal d'activation ![]() , l'apprentissage facilite et amplifie la transmission du neurone
, l'apprentissage facilite et amplifie la transmission du neurone ![]() vers le neurone
vers le neurone ![]() .
Sachant que les neurones afférents corrélés à
.
Sachant que les neurones afférents corrélés à ![]() sont également corrélés entre eux, le renforcement des liens en provenance de ce groupe de neurones accentue l'influence de leur signal commun sur le champ local du neurone
sont également corrélés entre eux, le renforcement des liens en provenance de ce groupe de neurones accentue l'influence de leur signal commun sur le champ local du neurone ![]() , ce qui a pour effet d'augmenter :
, ce qui a pour effet d'augmenter :
 .
.
Par ailleurs, on constate que l'évolution du régime dynamique est non-monotone.
On observe fréquemment une augmentation de la complexité de la dynamique qui va de pair avec l'augmentation du diamètre du signal ![]() , suivie d'une régularisation de la dynamique qui aboutit à un cycle de forte amplitude.
On peut voir cette évolution en deux étapes comme la manifestation de deux tendances concurrentes :
, suivie d'une régularisation de la dynamique qui aboutit à un cycle de forte amplitude.
On peut voir cette évolution en deux étapes comme la manifestation de deux tendances concurrentes :