La figure 4.3 présente un exemple de dynamique d'apprentissage, lorsque l'on place le réseau à la frontière du chaos.
Après 200 pas de temps de dynamique spontanée, on lance l'apprentissage sur 500 pas de temps, avec
![]() .
La pseudo-période initiale, très proche de
.
La pseudo-période initiale, très proche de ![]() , évolue en cours d'apprentissage. Après apprentissage, la dynamique est strictement périodique, de période
, évolue en cours d'apprentissage. Après apprentissage, la dynamique est strictement périodique, de période ![]() .
.
|
|
En renforçant le pouvoir excitateur des neurones les plus corrélés
au temps ![]() et le pouvoir inhibiteur
des neurones les plus anticorrélés au temps
et le pouvoir inhibiteur
des neurones les plus anticorrélés au temps ![]() ,
on tend à ce que l'activité de certains neurones au temps
,
on tend à ce que l'activité de certains neurones au temps ![]() dépende
plus fortement d'un groupe de neurones dont le signal est
fort et significatif au temps
dépende
plus fortement d'un groupe de neurones dont le signal est
fort et significatif au temps ![]() (qui eux mêmes dépendent de
l'activité simultanée d'un certain nombre de neurones au temps
(qui eux mêmes dépendent de
l'activité simultanée d'un certain nombre de neurones au temps 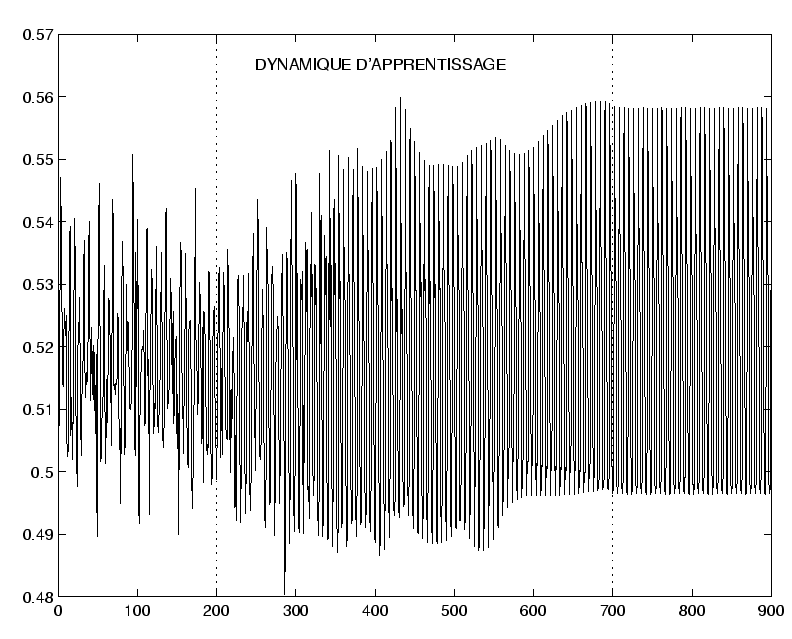 etc...).
Si une période sous-jacente existe dans le système, celle-ci sera renforcée,
l'activité du neurone devenant de proche en proche de plus en plus corrélée
à sa propre activité au temps
etc...).
Si une période sous-jacente existe dans le système, celle-ci sera renforcée,
l'activité du neurone devenant de proche en proche de plus en plus corrélée
à sa propre activité au temps ![]() .
Au contraire, si aucune périodicité n'existe au préalable,
les poids seront modifiés selon l'aléa de la dynamique
sans induire de modification significative sur le régime
pour des durées d'apprentissage de l'ordre de 500 pas de temps.
.
Au contraire, si aucune périodicité n'existe au préalable,
les poids seront modifiés selon l'aléa de la dynamique
sans induire de modification significative sur le régime
pour des durées d'apprentissage de l'ordre de 500 pas de temps.