Dynamique.

Pour $p\in \{1,..,K\}$ et $1\leq i\leq N^{(p)}$,

$$\left\{ \begin{array}{l} \displaystyle{\mathrm{pour\ } q\in \{1,.... ...a_i^{(p)}}\\ \displaystyle{x_i^{(p)}(t)=f_g(u_i^{(p)}(t))} \end{array} \right.$$ (5.1)

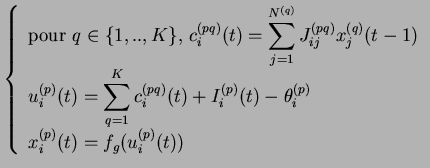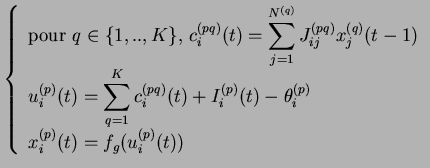Le champ local $c_i^{(pq)}(t)$ intègre les signaux en provenance de la population $q$ vers la population $p$. Le potentiel $u_i^{(p)}(t)$ est la somme des champs locaux $c_i^{(pq)}(t)$ et du signal externe $I_i^{(p)}(t)$, auquel on soustrait le seuil d'activation $\theta_i^{(p)}$. L'activation est notée par $x_i^{(p)}(t)$. $f_g$ est la fonction de transfert de $\mathbb{R}$ vers $]0,1[$. On prend toujours pour les simulations $f_g(x)=\frac{1+\tanh(gx)}{2}$, de gain $g/2$. Les valeurs des poids synaptiques et des seuils sont fixées à l'initialisation, et suivent respectivement les lois gaussiennes ${\mathcal N}(\frac{\bar{J}^{(pq)}}{N^{(q)}},\frac{{\sigma_J^{(pq)}}^{2}}{N^{(q)}})$ et ${\mathcal N}(\bar{\theta}^{(p)},{\sigma_\theta^{(p)}}^{2})$. 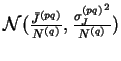Toutes ces variables aléatoires sont supposées indépendantes.

En régime stationnaire, on peut écrire :

$$\left\{ \begin{array}{l} u_i^{(p)}(t)={u_i^{(p)}}^*+b_i^{(p)}(t)\\ x_i^{(p)}(t)={x_i^{(p)}}^*+a_i^{(p)}(t) \end{array}\right.$$

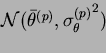
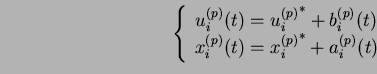Où ${u_i^{(p)}}^*$ est le potentiel moyen, $b_i^{(p)}(t)$ le signal propre, ${x_i^{(p)}}^*$ l'activation moyenne et $a_i^{(p)}(t)$ l'activité dynamique.