Apprentissage.

La règle d'apprentissage à $K$ populations repose exactement sur les mêmes principes que ceux appliqués au modèle à une population. La dynamique sur les couplages repose sur la conjonction des activités pré et post-synaptiques $a_i^{(p)}(t) a_j^{(q)}(t-1)$, avec un décalage d'un pas de temps représentant le délai de transmission.

$$J_{ij}^{(pq)}(t)=J_{ij}^{(pq)}(t-1)+\frac{\alpha^{(pq)}}{N^{(q)}} a_i^{(p)}(t) a_j^{(q)}(t-1)$$ (5.2)

La partie constante du signal d'activation ${x_i^{(p)}}^*$ est estimée à chaque instant par ${\tilde{x}_i^{(p)*}}(t)=(1-\beta) {\tilde{x}_i^{(p)*}}(t-1) + \beta \tilde{x}_i^{(p)}(t)$.

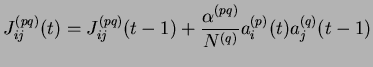Le paramètre qui règle l'intensité de l'apprentissage de $q$ vers $p$ est $\alpha^{(pq)}$. La modification des poids est normalisée en $1/N^{(q)}$, afin que l'impact moyen de la règle sur le champ local $c_{i}^{(pq)}$ soit indépendant de $N^{(q)}$. Pour une valeur d' $\alpha^{(pq)}$ fixée, plus la taille de la population $q$ est faible, plus l'impact de l'apprentissage sur un lien $J_{ij}^{(pq)}$ donné est élevé. Une valeur nulle d' $\alpha^{(pq)}$ interdit les modifications synaptiques entre la population $q$ et la population $p$ (lien non modifiable). Sur le modèle utilisé dans la suite de ce chapitre, on note $\alpha$ la valeur de référence telle que $\alpha^{(pq)}=\alpha$ pour toute classe de liens modifiables, et $\alpha^{(pq)}=0$ pour toute classe de liens non-modifiables.