Transformation de Fourier

Considérons un échantillon pour $t=1..T$ d'un signal $s(t)$, mono dimensionnel discret. L'intervalle entre deux valeurs successives est pris comme unité de temps. On souhaite connaître les caractéristiques de périodicité les plus significatives de ce signal.

Au signal $s$ correspond le spectre défini par :

$$\hat{s}(f)=\frac{1}{\sqrt{T}}\sum_{k=1}^{T}s(t)e^{-i\frac{2 \pi f t}{T}}$$

Le coefficient $\hat{s}(f)$ doit être associé à la fréquence $f=\frac{k}{T}$, à laquelle correspond la période ou pseudo période $\tau=\frac{T}{k}$.

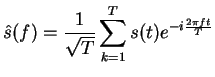
Le spectre de puissance est donné, pout tout $t$ par :

$$S(f)=\vert\hat{s}(f)\vert^2$$

où $\vert.\vert$ est la norme complexe. Le spectre de puissance donne pour toute valeur de la fréquence la puissance transportée par cette fréquence. Le terme ``puissance'' se rapporte à une énergie moyenne transportée par unité de temps, dans l'hypothèse où l'on peut associer un terme d'énergie au carré de l'amplitude du signal.

On a la propriété $S(f)=S(1-f)$. Sur un échantillon discret de taille $T$, le spectre nous donne les fréquences les plus saillantes du signal, comprises entre $\frac{1}{T}$ (période $T$) et $\frac{1}{2}$ (période 2). Le spectre de Fourier nous fournit une valeur approchée (avec une précision de l'ordre de $1/T$) de la fréquence principale et des fréquences secondaires du signal.

On représente souvent le spectre de puissance avec en abcisse la fréquence et en ordonnée la valeur de la puissance exprimée selon une échelle logarithmique (ce qui permet de mieux voir les continuités et discontinuités du spectre). La valeur de la puissance est divisée par la longueur de l'échantillon, et se ramène donc à l'énergie transportée en moyenne sur un pas de temps.