Le terme ``dynamique contrainte'' désigne un système sous la contrainte d'une influence extérieure, prenant la forme d'un signal ![]() .
L'expression du système devient donc :
.
L'expression du système devient donc :
On distinguera deux types d'entrées :
entrée statique si le signal est constant 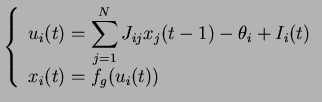 ,
entrée dynamique si le signal d'entrée est non constant.
Dans le cas d'une entrée statique définie selon un tirage gaussien
,
entrée dynamique si le signal d'entrée est non constant.
Dans le cas d'une entrée statique définie selon un tirage gaussien
![]() ,
, ![]() est comparable au seuil
est comparable au seuil ![]() , auquel il s'additionne linéairement.
Dans ce cas, la dynamique contrainte peut être décrite dans le cadre des équations de champ moyen et l'ajout d'un entrée correspond à un déplacement dans l'espace des paramètres selon les directions
, auquel il s'additionne linéairement.
Dans ce cas, la dynamique contrainte peut être décrite dans le cadre des équations de champ moyen et l'ajout d'un entrée correspond à un déplacement dans l'espace des paramètres selon les directions
![]() et
et
![]() .
.
Un motif d'entrée correspond, dans le cas d'un entrée statique, à un jeu de valeurs
![]() .
Un motif temporel correspond à une série de motifs,
.
Un motif temporel correspond à une série de motifs,
![]() ; un motif temporel périodique se caractérise par sa période
; un motif temporel périodique se caractérise par sa période ![]() .
.
Notre travail porte sur le régime stationnaire, ce qui signifie que toute étude sur les caractéristiques de la dynamique d'un réseau suppose l'élimination du régime transitoire. En régime stationnaire, on utilise la notation :
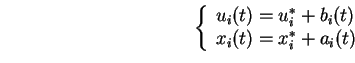 l'activation moyenne et
l'activation moyenne et
Cette notation se réfère, bien sûr, à la notation utilisée pour la description du processus gaussien stationnaire à la limite thermodynamique sur le modèle (voir page ![]() ).
Lorsque cette notation est étendue aux systèmes de taille finie, le signal
).
Lorsque cette notation est étendue aux systèmes de taille finie, le signal ![]() ne correspond plus à un bruit blanc, mais possède les caractéristiques du régime dynamique qui se développe dans le réseau.
ne correspond plus à un bruit blanc, mais possède les caractéristiques du régime dynamique qui se développe dans le réseau.