On a tracé, à taille finie, une courbe analogue à la ligne de bifurcation obtenue à la limite thermodynamique.
La taille finie permet de prendre en compte la largeur de la plage de déstabilisation (c'est à dire l'intervalle entre ![]() valeur de déstabilisation et
valeur de déstabilisation et ![]() valeur d'entrée dans le chaos).
Cette courbe se fonde sur les comportements observés sur 50 réseaux de 200 neurones tirés aléatoirement. Sur chacun de ces réseaux, on mesure la valeur de
valeur d'entrée dans le chaos).
Cette courbe se fonde sur les comportements observés sur 50 réseaux de 200 neurones tirés aléatoirement. Sur chacun de ces réseaux, on mesure la valeur de ![]() (méthode du plus grand exposant de Lyapunov), ainsi que la valeur de
(méthode du plus grand exposant de Lyapunov), ainsi que la valeur de ![]() (déstabilisation de la jacobienne), pour des motifs dont l'écart-type
(déstabilisation de la jacobienne), pour des motifs dont l'écart-type ![]() varie entre 0 ( pas de motif) et 1.
Pour chaque
varie entre 0 ( pas de motif) et 1.
Pour chaque ![]() , ces valeurs sont moyennées sur les 50 réseaux.
On obtient la figure 3.21.
, ces valeurs sont moyennées sur les 50 réseaux.
On obtient la figure 3.21.
![\includegraphics[]{route_inv.eps}](img819.png) |
On voit donc :
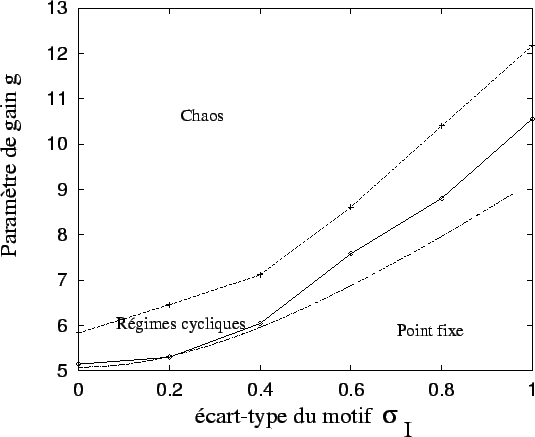 , les valeurs empiriques de déstabilisation sont très proches de la valeur théorique.
La longueur de la plage de transition
, les valeurs empiriques de déstabilisation sont très proches de la valeur théorique.
La longueur de la plage de transition
En tenant le même raisonnement que précédemment, on voit que l'augmentation de l'écart-type ![]() d'un motif donné (déplacement vers la droite du diagramme) tend à induire une route par quasi-périodicité inverse.
La seule différence est que dans ce cas, on ne garde pas l'homogénéité de la période fondamentale et de l'organisation dynamique.
d'un motif donné (déplacement vers la droite du diagramme) tend à induire une route par quasi-périodicité inverse.
La seule différence est que dans ce cas, on ne garde pas l'homogénéité de la période fondamentale et de l'organisation dynamique.
La figure 3.22 permet mettre en évidence cette route par quasi-périodicité inverse sur un exemple particulier.
Un motif ![]() qui nous sert de référence est tiré selon une loi normale centrée.
La figure donne l'évolution de la dynamique contrainte par le motif
qui nous sert de référence est tiré selon une loi normale centrée.
La figure donne l'évolution de la dynamique contrainte par le motif
![]() , pour des valeurs croissantes de
, pour des valeurs croissantes de ![]() .
Une simplification de la dynamique est ainsi mise en évidence.
Celle-ci aboutit dans tous les cas à un point fixe (qui n'est pas montré sur la figure).
.
Une simplification de la dynamique est ainsi mise en évidence.
Celle-ci aboutit dans tous les cas à un point fixe (qui n'est pas montré sur la figure).
![\includegraphics[]{ko_inverse_2.eps}](img826.png)
![\includegraphics[]{ko_inverse_3.eps}](img827.png)
|
Ce comportement systématique de simplification de la dynamique pour ![]() croissant observé sur les motifs centrés se complique singulièrement lorsque l'on effectue la même opération sur des motifs non centrés, avec un facteur de dilatation sur la dispersion
croissant observé sur les motifs centrés se complique singulièrement lorsque l'on effectue la même opération sur des motifs non centrés, avec un facteur de dilatation sur la dispersion
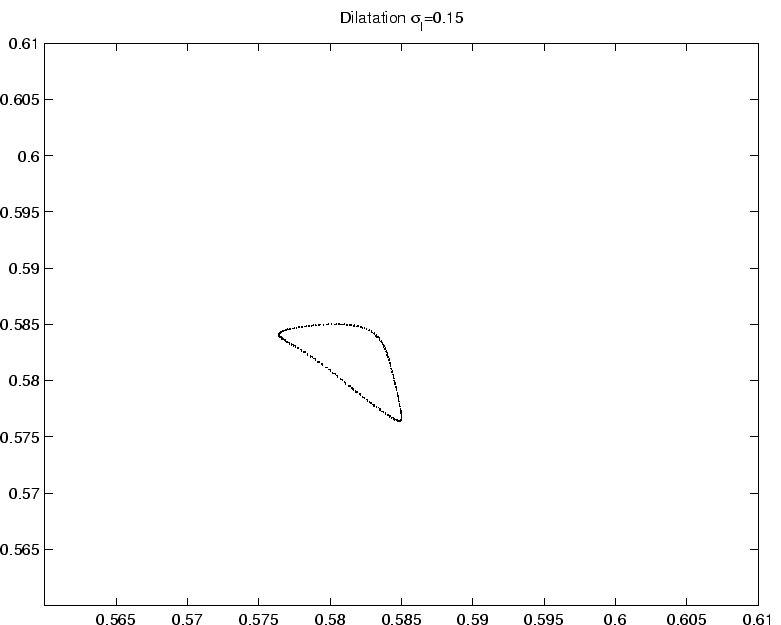 .
.
Sur un réseau donné, on voit que la valeur d'entrée dans le chaos varie de manière non-monotone lorsque l'on augmente ![]() .
Le comportement non-monotone de la figure 3.23) peut être comparé avec le comportement monotone croissant obtenu à la limite thermodynamique de la figure 3.19 (sachant que ce comportement monotone croissant se maintient pour la valeur
.
Le comportement non-monotone de la figure 3.23) peut être comparé avec le comportement monotone croissant obtenu à la limite thermodynamique de la figure 3.19 (sachant que ce comportement monotone croissant se maintient pour la valeur
![]() utilisée).
Ainsi, lorsque l'on augmente
utilisée).
Ainsi, lorsque l'on augmente ![]() à
à ![]() fixé (par exemple
fixé (par exemple ![]() ), on peut observer des allers retours entre des régimes chaotiques, cycliques et de point fixe.
), on peut observer des allers retours entre des régimes chaotiques, cycliques et de point fixe.
|
|
Sachant que la valeur de déstabilisation dépend fortement de la configuration spatiale et donc des valeurs des potentiels ![]() , on a ici l'illustration du fait que la dilatation d'un motif non centré a des répercussions très variées sur cette configuration spatiale, et donc sur l'effectif des neurones actifs qui entretiennent la dynamique.
L'augmentation de
, on a ici l'illustration du fait que la dilatation d'un motif non centré a des répercussions très variées sur cette configuration spatiale, et donc sur l'effectif des neurones actifs qui entretiennent la dynamique.
L'augmentation de ![]() fait transiter les neurones à travers la zone où ils sont actifs dynamiquement (c.à.d où leur potentiel moyen est proche de zéro).
L'augmentation de
fait transiter les neurones à travers la zone où ils sont actifs dynamiquement (c.à.d où leur potentiel moyen est proche de zéro).
L'augmentation de ![]() produit ainsi un renouvellement de l'effectif des neurones actifs qui peut induire le développement de régimes dynamiques nouveaux.
produit ainsi un renouvellement de l'effectif des neurones actifs qui peut induire le développement de régimes dynamiques nouveaux.