




suivant: Effet sur la valeur
monter: Présentation de motifs dynamiques
précédent: Présentation de motifs dynamiques
Table des matières
Index
Lorsqu'un motif dynamique est imposé, celui-ci alimente de l'extérieur la dynamique du réseau.
Le système n'est donc plus autonome.
Il s'instaure donc une forme de concurrence entre le régime dynamique périodique imposé et celui qui se développe spontanément dans le système.
On peut noter qu'il n'y a plus de régime de point fixe, quelle que soit la valeur de  ,
,
Pour des séquences de motifs tels que 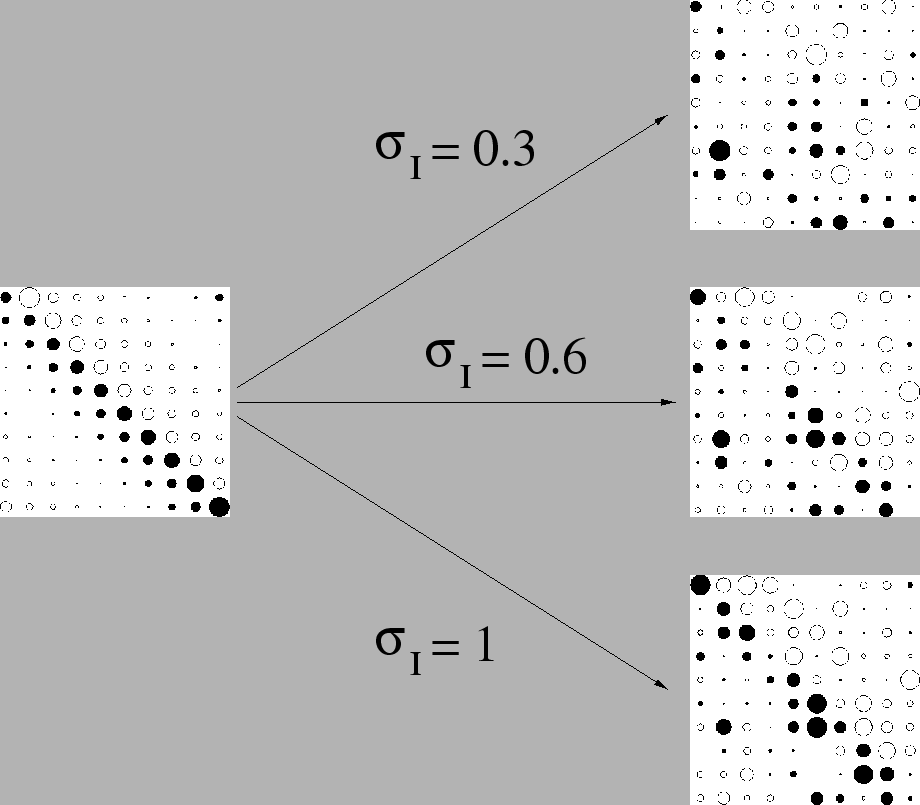 ,
,
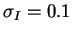 , on observe en général le comportement suivant (voir figure 3.26) :
, on observe en général le comportement suivant (voir figure 3.26) :
- Pour les valeurs de
 correspondant au point fixe en dynamique spontanée, la dynamique contrainte est strictement périodique.
La dynamique du réseau est passive et se laisse guider par le signal d'entrée.
Si la période de l'entrée est
correspondant au point fixe en dynamique spontanée, la dynamique contrainte est strictement périodique.
La dynamique du réseau est passive et se laisse guider par le signal d'entrée.
Si la période de l'entrée est  entière, la dynamique passe strictement par une séquence de
entière, la dynamique passe strictement par une séquence de  états dynamiques distincts.
états dynamiques distincts.
- Pour les valeurs de
 correspondant au régime pseudo-périodique en dynamique spontanée, on observe
correspondant au régime pseudo-périodique en dynamique spontanée, on observe 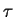 cycles distincts sur un diagramme de premier retour du signal moyen. Le cycle est dupliqué
cycles distincts sur un diagramme de premier retour du signal moyen. Le cycle est dupliqué 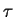 fois.
fois.
- Pour les valeurs de
 correspondant au régime chaotique en dynamique spontanée, on observe sur le diagramme de premier retour, à la frontière du chaos,
correspondant au régime chaotique en dynamique spontanée, on observe sur le diagramme de premier retour, à la frontière du chaos, 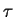 régions où la densité de points est plus importante, qui sont des reliquats des cycles atteints à la déstabilisation. Pour des valeurs de
régions où la densité de points est plus importante, qui sont des reliquats des cycles atteints à la déstabilisation. Pour des valeurs de  plus élevées, on ne parvient plus à distinguer à l'oeil la périodicité du motif (bien que celle-ci reste décelable par spectre de puissance pour toute valeur de
plus élevées, on ne parvient plus à distinguer à l'oeil la périodicité du motif (bien que celle-ci reste décelable par spectre de puissance pour toute valeur de  ).
).
Plus  augmente, plus la dynamique interne semble donc prendre le pas sur la dynamique imposée.
augmente, plus la dynamique interne semble donc prendre le pas sur la dynamique imposée.
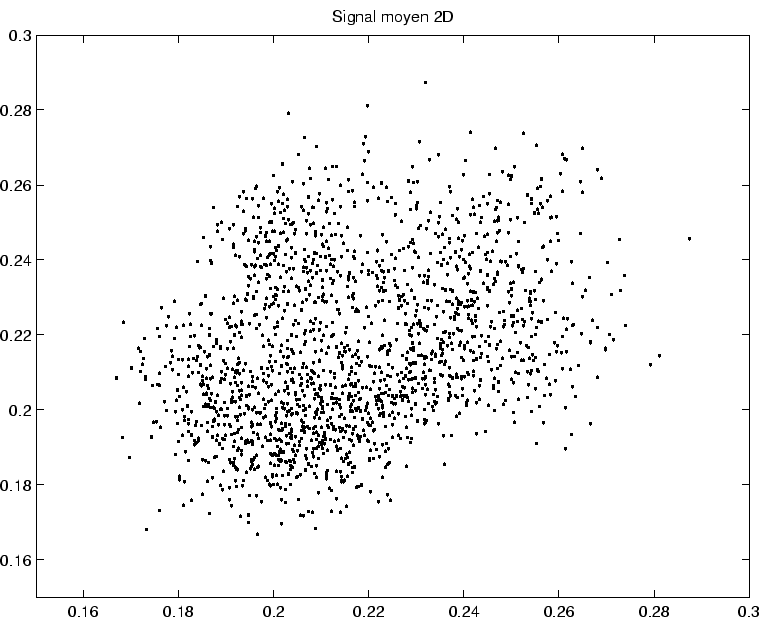
Figure 3.26:
Route vers le chaos avec un signal d'entrée périodique.
La période imposée est 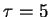 .
On a représenté les diagrammes de premier retour du signal
.
On a représenté les diagrammes de premier retour du signal  .
Les valeurs de
.
Les valeurs de  sont successivement
sont successivement  (
(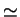 point fixe),
point fixe), 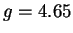 (cycles limites),
(cycles limites), 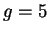 (frontière du chaos),
(frontière du chaos), 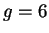 (chaos profond).
On constate, en dynamique pseudo-périodique et à la frontière du chaos, que la disposition des amas de points reproduit celle observée pour
(chaos profond).
On constate, en dynamique pseudo-périodique et à la frontière du chaos, que la disposition des amas de points reproduit celle observée pour  .
Paramètres :
.
Paramètres :  ,
,  ,
,
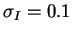 ,
,
 ,
,
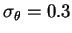 ,
, 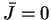 ,
,
 .
.
|
|





suivant: Effet sur la valeur
monter: Présentation de motifs dynamiques
précédent: Présentation de motifs dynamiques
Table des matières
Index
Dauce Emmanuel
2003-05-07
![]() ,
,
 ,
,
![]() , on observe en général le comportement suivant (voir figure 3.26) :
, on observe en général le comportement suivant (voir figure 3.26) :
![]() augmente, plus la dynamique interne semble donc prendre le pas sur la dynamique imposée.
augmente, plus la dynamique interne semble donc prendre le pas sur la dynamique imposée.
![\includegraphics[]{dyn_cycle_seq.eps}](img843.png)
![\includegraphics[]{dyn_frontko_seq.eps}](img844.png)
![\includegraphics[]{dyn_ko_seq.eps}](img845.png)