 .
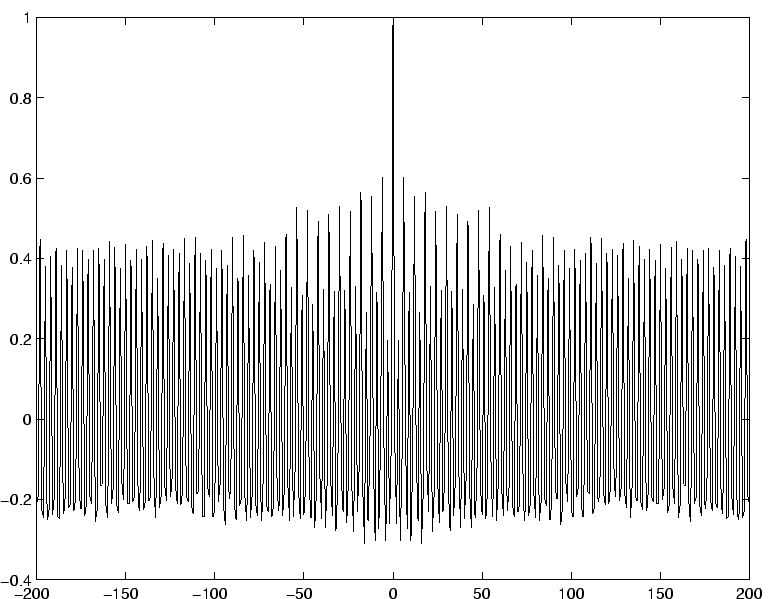
Néanmoins, cette pulsation fondamentale n'est pas nécessairement celle qui domine le spectre de puissance.
On constate que le système favorise indifféremment la fréquence fondamentale ou l'une de ses harmoniques.
Bien sûr, plus la valeur de
.
Néanmoins, cette pulsation fondamentale n'est pas nécessairement celle qui domine le spectre de puissance.
On constate que le système favorise indifféremment la fréquence fondamentale ou l'une de ses harmoniques.
Bien sûr, plus la valeur de
Lorsqu'un motif de période ![]() est présenté en entrée, cette période tend à imposer la fréquence fondamentale du spectre de puissance
est présenté en entrée, cette période tend à imposer la fréquence fondamentale du spectre de puissance  .
Néanmoins, cette pulsation fondamentale n'est pas nécessairement celle qui domine le spectre de puissance.
On constate que le système favorise indifféremment la fréquence fondamentale ou l'une de ses harmoniques.
Bien sûr, plus la valeur de
.
Néanmoins, cette pulsation fondamentale n'est pas nécessairement celle qui domine le spectre de puissance.
On constate que le système favorise indifféremment la fréquence fondamentale ou l'une de ses harmoniques.
Bien sûr, plus la valeur de ![]() est grande, plus le risque de voir se développer un régime dont la période est fondée sur l'un de ces harmoniques est grande.
est grande, plus le risque de voir se développer un régime dont la période est fondée sur l'un de ces harmoniques est grande.
La période ``capturée'' est donc celle qui domine le spectre.
Pour mesurer les caractéristiques de cette capture, on définit des séquences de motifs aléatoires pour des périodes allant de 2 à 12.
Chaque motif est défini selon les paramètres  ,
,
![]() .
Pour chaque valeur de
.
Pour chaque valeur de ![]() , on tire différents couples (Réseau, Séquence), et on mesure la période capturée.
Les valeurs trouvées sont alors réparties sur un histogramme (voir figure 3.29).
, on tire différents couples (Réseau, Séquence), et on mesure la période capturée.
Les valeurs trouvées sont alors réparties sur un histogramme (voir figure 3.29).
![\includegraphics[]{hist_periode_3.eps}](img851.png)
![\includegraphics[]{hist_periode_4.eps}](img852.png)
![\includegraphics[]{hist_periode_6.eps}](img853.png)
![\includegraphics[]{hist_periode_8.eps}](img854.png)
![\includegraphics[]{hist_periode_12.eps}](img855.png)
|
On voit donc que pour des séquences de période 2 ou 3, la capture est conforme à la période imposée. Il existe néanmoins une minorité de réseaux pour lesquels une autre période reste dominante dans le spectre. On peut penser que celle-ci correspond soit à la période de la dynamique spontanée, soit à un multiple de la période imposée.
À partir de ![]() , on commence à observer des phénomènes de résonnance.
Dans presque la moitié des cas, l'harmonique 2 est dominante.
Ce choix indifférent entre la période fondamentale et ses harmoniques semble réduire les chances de capter la période fondamentale lorsque
, on commence à observer des phénomènes de résonnance.
Dans presque la moitié des cas, l'harmonique 2 est dominante.
Ce choix indifférent entre la période fondamentale et ses harmoniques semble réduire les chances de capter la période fondamentale lorsque ![]() augmente.
Par exemple, pour un signal de période
augmente.
Par exemple, pour un signal de période ![]() , la probabilité d'apparition associée à la période
, la probabilité d'apparition associée à la période ![]() est à peu près égale à la probabilité d'apparition de chacun de ses harmoniques 6, 4, 3 et 2.
est à peu près égale à la probabilité d'apparition de chacun de ses harmoniques 6, 4, 3 et 2.
Si, par exemple, l'harmonique ![]() domine le spectre pour une stimulation de période
domine le spectre pour une stimulation de période ![]() , et que le système tend à produire un circuit d'activation de période 4, on peut dire qu'il ``interprète'' de la même façon sur ses sorties les 3 séquences de période 4 qui forment la séquence complète.
, et que le système tend à produire un circuit d'activation de période 4, on peut dire qu'il ``interprète'' de la même façon sur ses sorties les 3 séquences de période 4 qui forment la séquence complète.