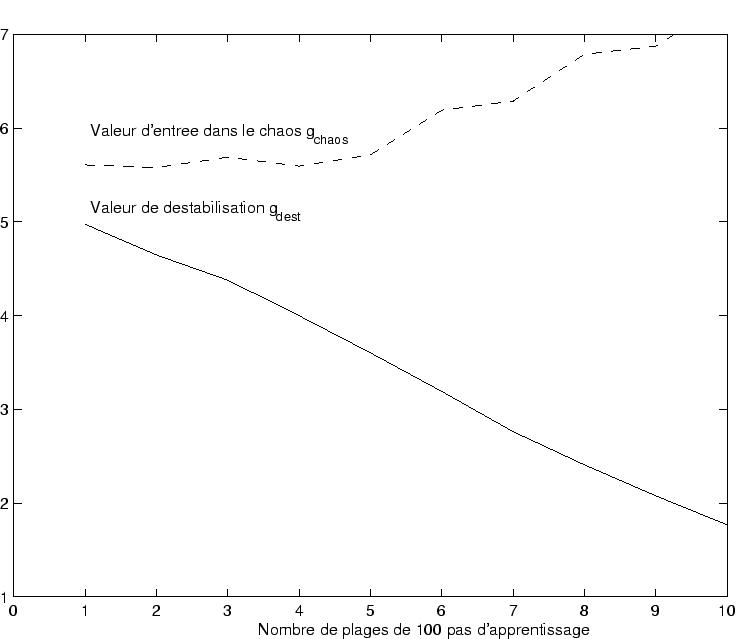
 .
L'observation de la matrice
.
L'observation de la matrice
Après apprentissage, on observe une augmentation faible, mais sensible et systématique, de la variance empirique de la distribution des poids.
Si ![]() marque le début de l'apprentissage et
marque le début de l'apprentissage et ![]() est la durée de l'apprentissage, on définit la matrice d'évolution des poids synaptiques
par
est la durée de l'apprentissage, on définit la matrice d'évolution des poids synaptiques
par
 .
L'observation de la matrice
.
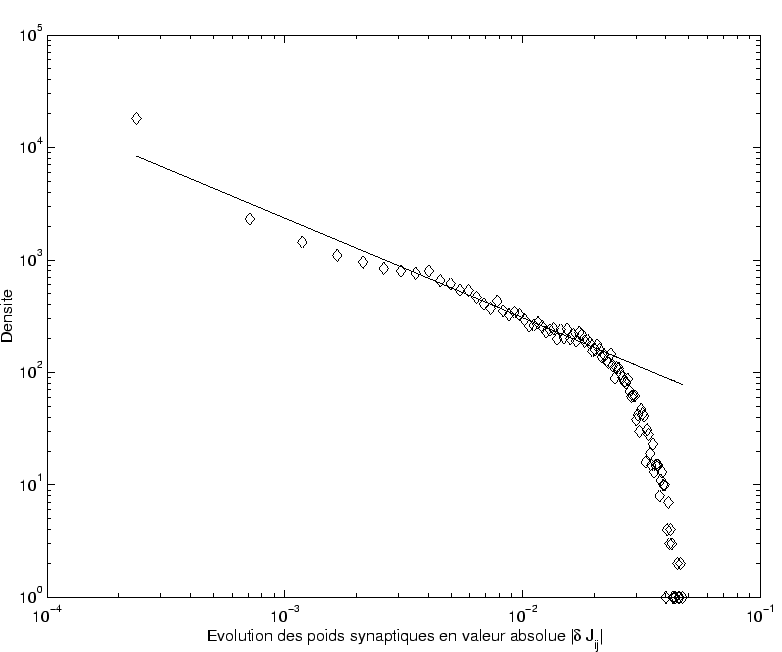
L'observation de la matrice ![]() montre que la répartition des valeurs n'est pas du tout uniforme.
Sachant que la modification des poids est proportionnelle à
cov
montre que la répartition des valeurs n'est pas du tout uniforme.
Sachant que la modification des poids est proportionnelle à
cov![]() , dont la distribution suit une loi de puissance avant apprentissage, la répartition des
, dont la distribution suit une loi de puissance avant apprentissage, la répartition des
![]() correspond logiquement à une loi de puissance (voir figure 4.5).
On voit que la modification de variance observée de manière globale, correspond localement à des augmentations fortes et ciblées sur certains liens synaptiques spécifiques et rares.
correspond logiquement à une loi de puissance (voir figure 4.5).
On voit que la modification de variance observée de manière globale, correspond localement à des augmentations fortes et ciblées sur certains liens synaptiques spécifiques et rares.
|
|
Par ailleurs, les liens renforcés correspondent au circuit d'activation spécifique de la dynamique spontanée du réseau.
Dans le cas où ![]() est proche de 2, par exemple, la matrice
est proche de 2, par exemple, la matrice ![]() est à peu près symétrique (renforcement des signaux en opposition de phase).
Dans le cas où la période
est à peu près symétrique (renforcement des signaux en opposition de phase).
Dans le cas où la période ![]() est proche de 4, la matrice
est proche de 4, la matrice ![]() est à peu près antisymétrique (renforcement des signaux en quadrature).
Globalement, une forte valeur de
est à peu près antisymétrique (renforcement des signaux en quadrature).
Globalement, une forte valeur de
![]() indique un décalage
de phase de 1 entre le signal de
indique un décalage
de phase de 1 entre le signal de ![]() et celui de
et celui de ![]() .
La règle a plus généralement tendance à renforcer la connectivité positive entre les relais du circuit interne dont le décalage de phase vaut 1
(et la connectivité négative entre les relais
dont le décalage de phase vaut environ
.
La règle a plus généralement tendance à renforcer la connectivité positive entre les relais du circuit interne dont le décalage de phase vaut 1
(et la connectivité négative entre les relais
dont le décalage de phase vaut environ
 ).
).
L'étude de la matrice ![]() permet d'observer la mise en place de circuits d'activation qui relient entre eux des groupes de neurones corrélés avec un décalage d'un pas de temps.
Chaque colonne (d'indice
permet d'observer la mise en place de circuits d'activation qui relient entre eux des groupes de neurones corrélés avec un décalage d'un pas de temps.
Chaque colonne (d'indice ![]() ) de la matrice contient des valeurs significativement plus élevées que la moyenne qui désignent les neurones cibles
) de la matrice contient des valeurs significativement plus élevées que la moyenne qui désignent les neurones cibles ![]() que le neurone source
que le neurone source ![]() active préférentiellement.
On peut ainsi définir un graphe où apparaît le chemin complet, dont la longueur doit correspondre à la période fondamentale.
Le schéma de la figure 4.6 illustre ce principe de renforcement, pour 5 neurones et une période
active préférentiellement.
On peut ainsi définir un graphe où apparaît le chemin complet, dont la longueur doit correspondre à la période fondamentale.
Le schéma de la figure 4.6 illustre ce principe de renforcement, pour 5 neurones et une période ![]() .
.
|
|