Les notions d'énergie introduites page ![]() , peuvent également être utilisées dans le cadre de l'apprentissage pour mesurer l'évolution de l'amplitude des signaux individuels.
À partir du terme de transfert d'énergie
, peuvent également être utilisées dans le cadre de l'apprentissage pour mesurer l'évolution de l'amplitude des signaux individuels.
À partir du terme de transfert d'énergie
![]() cov
cov![]() , il est possible en effet d'estimer un terme d'énergie local à chaque neurone caractéristique de l'amplitude du signal produit localement.
, il est possible en effet d'estimer un terme d'énergie local à chaque neurone caractéristique de l'amplitude du signal produit localement.
On a donc
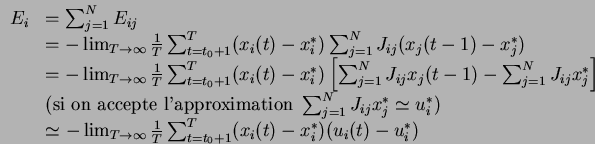 cov
cov![]() .
Les signaux
.
Les signaux ![]() et
et ![]() étant fortement corrélés, le terme d'énergie locale donne tout simplement une indication sur l'amplitude du signal produit, en tenant à la fois compte de la variance du signal de potentiel, qui est assez homogène d'un neurone à l'autre, et de celle du signal d'activation, qui est importante si le neurone est actif et très faible si le neurone est inactif.
En conséquence, les neurones inactifs, muets ou saturés, ont un terme d'énergie local très faible.
Les neurones actifs sont ceux qui concentrent l'essentiel des valeurs de l'énergie.
étant fortement corrélés, le terme d'énergie locale donne tout simplement une indication sur l'amplitude du signal produit, en tenant à la fois compte de la variance du signal de potentiel, qui est assez homogène d'un neurone à l'autre, et de celle du signal d'activation, qui est importante si le neurone est actif et très faible si le neurone est inactif.
En conséquence, les neurones inactifs, muets ou saturés, ont un terme d'énergie local très faible.
Les neurones actifs sont ceux qui concentrent l'essentiel des valeurs de l'énergie.
Le terme global d'énergie
![]() donne quant à lui une indication sur l'amplitude moyenne de chaque signal individuel.
donne quant à lui une indication sur l'amplitude moyenne de chaque signal individuel.
La modification des liens synaptiques se fonde comme on l'a vu sur la covariance entre neurone afférent et neurone récepteur. Tous les neurones actifs dans le réseau subissent une augmentation de l'amplitude de leur signal d'activation, qui se traduit également par une augmentation de la valeur de la covariance entre le neurone et ses prédécesseurs. La Figure 4.7 montre l'évolution du terme d'énergie globale en cours d'apprentissage. Celui-ci tend à augmenter en valeur absolue, au cours de l'apprentisage, à vitesse exponentielle en fonction du nombre de pas d'apprentissage. L'apprentissage semble ainsi produire une réaction en chaîne qui conduit à une augmentation exponentielle de l'amplitude des signaux d'activation individuels.
|
|
Pour l'exemple présenté figure 4.3, la valeur de l'énergie totale passe de -4 à -46.5, soit globalement multipliée par 10.
Chaque terme de transfert d'énergie
![]() cov
cov![]() dépend linéairement de la covariance et voit son amplitude augmenter dans les mêmes proportions au cours de l'apprentissage.
Ainsi, la répartition des
dépend linéairement de la covariance et voit son amplitude augmenter dans les mêmes proportions au cours de l'apprentissage.
Ainsi, la répartition des ![]() subit une dilatation du même ordre, comme on peut le voir sur la figure 4.8.
L'assymétrie de la distribution se maintient, et la proportion de liens frustrés reste à peu près la même.
subit une dilatation du même ordre, comme on peut le voir sur la figure 4.8.
L'assymétrie de la distribution se maintient, et la proportion de liens frustrés reste à peu près la même.
![\includegraphics[]{app_fru_0.eps}](img935.png)
![\includegraphics[]{app_fru_500.eps}](img936.png)
|
On a vu dans les parties précédentes qu'il subsistait à la frontière du chaos une périodicité résiduelle. L'effet de l'apprentissage est de renforcer cette périodicité, et de mener progressivement d'une dynamique chaotique à une dynamique cyclique. La présence d'une périodicité résiduelle est une condition nécessaire pour que l'apprentissage fondé sur la dynamique spontanée ait un effet sensible sur le régime. Plus on est loin de la frontière du chaos, plus il faut itérer longtemps l'apprentissage pour produire un régime cyclique.
L'étude de la dynamique d'apprentissage sans stimulation extérieure permet de montrer le mode d'action de la règle, à savoir :