Nature de l'information contenue dans les signaux.

Les informations produites en entrée du réseau ont été classées en trois catégories, suivant un degré croissant de complexité :

1. Séquences non ambiguës : une séquence est caractérisée par une série $s_\tau=(i_1,...,i_\tau)$. Pour que la séquence soit non-ambiguë, on suppose de plus que tous les $i_k$ sont différents, $1 \leq k \leq \tau$. La stimulation du neurone $i_k$ est suivie par celle du neurone $i_{k+1}$ à l'instant suivant, pour $1 \leq k \leq \tau-1$, et la stimulation du neurone $i_\tau$ est suivie par celle du neurone $i_1$. 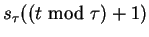Le signal $I^{(1)}(t)$ est donc périodique de période $\tau$.
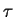2. Séquences ambiguës : les $i_k$ ne sont pas nécessairement différents : un même neurone peut apparaître plusieurs fois dans la séquence (voir aussi page ). Pour lever l'ambiguïté, il est nécessaire de faire appel à une information antérieure à la prémisse $i_k$, c'est à dire de mémoriser un ou plusieurs états plus anciens. Par exemple, sur la séquence $s_4=(1,1,2,2)$, la prémisse 1 est suivie par un 1 ou par un 2 suivant le contexte. Il est nécessaire d'avoir en mémoire l'état qui précède cette prémisse pour lever l'ambiguïté. Le degré d'une séquence est caractérisé par le nombre d'états antérieurs à la prémisse qu'il faut mémoriser pour lever toutes les ambiguïtés [62]. Par exemple, la séquence $s_4=(1,1,2,2)$ est de degré 1, et la séquence $s_8=(1,2,3,1,2,3,4,4)$ est de degré 3 (pour savoir si la prémisse 3 est suivie d'un 1 ou d'un 4, il faut mémoriser trois états antérieurs).
3. associations statiques/dynamiques : Lorsque les stimuli conditionnants sont pris en compte en tant que signal ``interne'', l'apprentissage porte sur une association $(s_{\tau_m,m}(t),D_m)$ où $s_{\tau_m,m}(t\ \mathrm{mod}\ \tau+1)$ définit le signal $I_m^{(1)}(t)$ projeté sur la couche primaire et 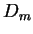$D_m$ désigne le motif conditionnant présent sur la couche dynamique tel que pendant l'apprentissage de la séquence, $\forall t, I_m^{(2)}(t)=D_m$.