




suivant: Séquences ambiguës
monter: Apprentissage de séquences
précédent: Apprentissage sur les liens
Table des matières
Index
Le dépassement du nombre de présentations critique
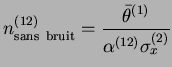 n'est pas le seul facteur qui limite la qualité de la réponse fournie par le réseau.
La longueur de la séquence à apprendre semble un facteur limitatif important.
Le système a des difficultés pour apprendre des séquences trop longues.
Cette difficulté repose sur les limitations de la couche dynamique en termes de capture de fréquence.
On a vu page
n'est pas le seul facteur qui limite la qualité de la réponse fournie par le réseau.
La longueur de la séquence à apprendre semble un facteur limitatif important.
Le système a des difficultés pour apprendre des séquences trop longues.
Cette difficulté repose sur les limitations de la couche dynamique en termes de capture de fréquence.
On a vu page ![[*]](/usr/share/latex2html/icons/crossref.png) que la présentation d'une stimulation de période
que la présentation d'une stimulation de période 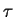 peut produire sur la couche dynamique un signal dont la fréquence dominante du spectre est un harmonique de la fréquence fondamentale
peut produire sur la couche dynamique un signal dont la fréquence dominante du spectre est un harmonique de la fréquence fondamentale 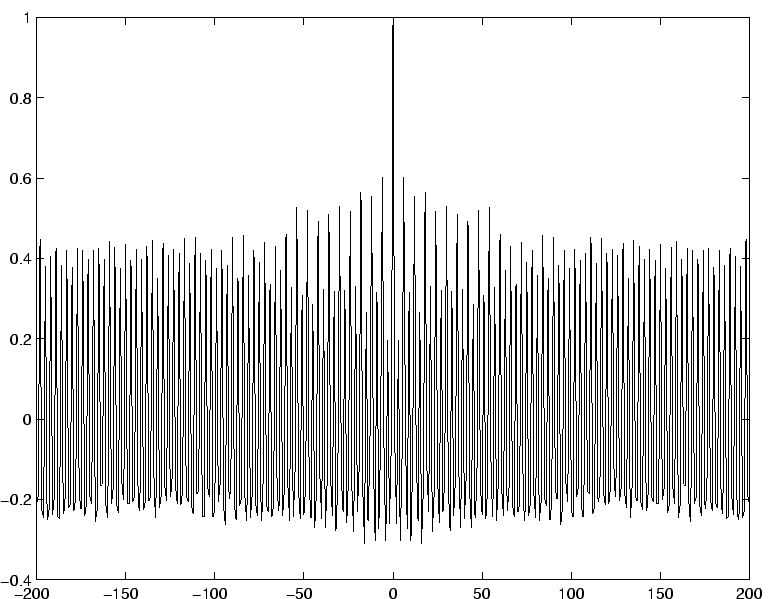 .
Pour des valeurs de
.
Pour des valeurs de 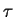 petites, c'est à dire inférieures à 8-10, la fréquence fondamentale reste significativement présente dans le spectre issu du signal moyen
petites, c'est à dire inférieures à 8-10, la fréquence fondamentale reste significativement présente dans le spectre issu du signal moyen  , ce qui assure, avec une bonne probabilité, que certains neurones possèdent cette fréquence fondamentale dans leur signal d'activation
, ce qui assure, avec une bonne probabilité, que certains neurones possèdent cette fréquence fondamentale dans leur signal d'activation 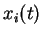 .
Il est encore possible dans ces conditions d'obtenir la restitution de la séquence complète à partir de l'activité de la couche dynamique.
Plus
.
Il est encore possible dans ces conditions d'obtenir la restitution de la séquence complète à partir de l'activité de la couche dynamique.
Plus 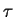 augmente, plus il devient difficile d'obtenir une bonne restitution.
Le système peut alors produire des motifs d'activation très proches pour deux motifs élémentaires distincts de la séquence d'entrée.
Dans ces conditions, la discrimination n'est plus possible.
Les figures
augmente, plus il devient difficile d'obtenir une bonne restitution.
Le système peut alors produire des motifs d'activation très proches pour deux motifs élémentaires distincts de la séquence d'entrée.
Dans ces conditions, la discrimination n'est plus possible.
Les figures ![[*]](/usr/share/latex2html/icons/crossref.png) et
et ![[*]](/usr/share/latex2html/icons/crossref.png) montrent l'évolution de la qualité de la reponse en fonction de la longueur de la séquence que l'on veut apprendre.
La qualité de la réponse tend à décroître avec la longueur de la séquence à apprendre.
montrent l'évolution de la qualité de la reponse en fonction de la longueur de la séquence que l'on veut apprendre.
La qualité de la réponse tend à décroître avec la longueur de la séquence à apprendre.
Figure:
Décroissance du taux de réussite selon la longueur de la séquence. Pour chaque valeur de 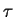 comprise entre 4 et 50, la figure donne les taux de réussite pour un apprentissage effectué en 30 présentations, en moyenne sur 50 réseaux. En ligne pleine :
comprise entre 4 et 50, la figure donne les taux de réussite pour un apprentissage effectué en 30 présentations, en moyenne sur 50 réseaux. En ligne pleine :
 . Pointillé long :
. Pointillé long :
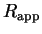 . Pointillé fin :
. Pointillé fin :
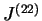 . Paramètres
. Paramètres
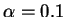 ,
, 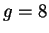 ,
,
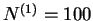 ,
,
 .
.
|
|
Figure:
Évolution du taux de réussite pour une séquence de longueur 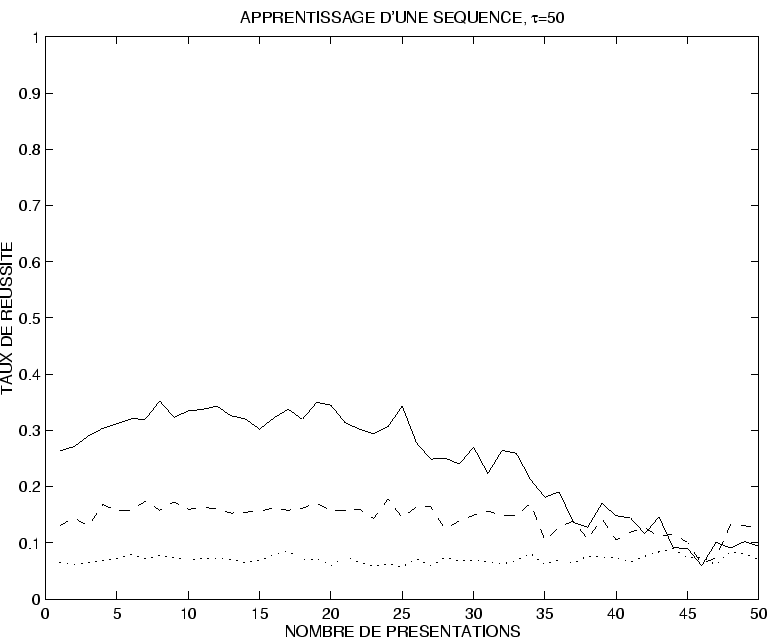 . La figure donne l'évolution en fonction du nombre de pas d'apprentissage des trois taux de réussite. En ligne pleine :
. La figure donne l'évolution en fonction du nombre de pas d'apprentissage des trois taux de réussite. En ligne pleine :
 . Pointillé long :
. Pointillé long :
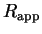 . Pointillé fin :
. Pointillé fin :
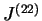 . Paramètres
. Paramètres
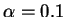 ,
, 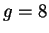 ,
,
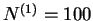 ,
,
 .
.
|
|
À ce stade, il semble que notre réseau soit plus adapté à l'apprentissage de nombreuses séquences assez courtes qu'à celui d'une seule séquence très longue 5.3.
Avant de regarder comment il est possible d'apprendre plusieurs séquences à un même réseau, on se penche tout d'abord sur l'apprentissage de séquences ambiguës temporellement.





suivant: Séquences ambiguës
monter: Apprentissage de séquences
précédent: Apprentissage sur les liens
Table des matières
Index
Dauce Emmanuel
2003-05-07
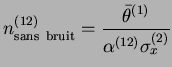 n'est pas le seul facteur qui limite la qualité de la réponse fournie par le réseau.
La longueur de la séquence à apprendre semble un facteur limitatif important.
Le système a des difficultés pour apprendre des séquences trop longues.
Cette difficulté repose sur les limitations de la couche dynamique en termes de capture de fréquence.
On a vu page
n'est pas le seul facteur qui limite la qualité de la réponse fournie par le réseau.
La longueur de la séquence à apprendre semble un facteur limitatif important.
Le système a des difficultés pour apprendre des séquences trop longues.
Cette difficulté repose sur les limitations de la couche dynamique en termes de capture de fréquence.
On a vu page  .
Pour des valeurs de
.
Pour des valeurs de  . La figure donne l'évolution en fonction du nombre de pas d'apprentissage des trois taux de réussite. En ligne pleine :
. La figure donne l'évolution en fonction du nombre de pas d'apprentissage des trois taux de réussite. En ligne pleine :
![\includegraphics[]{stat_tau50_refl.eps}](img1150.png)