




suivant: Exposants de Lyapunov
monter: Outils numériques
précédent: Fonction d'auto-corrélation
Table des matières
Index
Nombre de rotation
Étant donné un signal  , on appelle nombre de rotation
, on appelle nombre de rotation  la quantité
la quantité
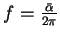 , où
, où
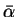 est l'angle moyen formé entre des triplets de points successifs de la dynamique, sur toute la trajectoire dans l'espace des phases.
Si
est l'angle moyen formé entre des triplets de points successifs de la dynamique, sur toute la trajectoire dans l'espace des phases.
Si  est mono dimensionnel, le nombre de rotation est également défini dans l'espace de premier retour, auquel cas les coordonnées des points des triplets sont (
est mono dimensionnel, le nombre de rotation est également défini dans l'espace de premier retour, auquel cas les coordonnées des points des triplets sont ( ,
, 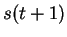 ), (
), (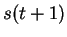 ,
, 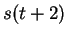 ), (
), (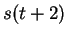 ,
,  ).
).
Pour une dynamique cyclique, 2 cas se présentent :
- Si
 est rationnel, le cycle est accroché et la dynamique passe par un nombre fini de valeurs. Sa périodicité est une valeur entière, donnée par le dénominateur de
est rationnel, le cycle est accroché et la dynamique passe par un nombre fini de valeurs. Sa périodicité est une valeur entière, donnée par le dénominateur de  .
Le numérateur de
.
Le numérateur de  donne le nombre de tours effectués sur l'attracteur avant de rejoindre le point de départ
(voir figure 1.1).
donne le nombre de tours effectués sur l'attracteur avant de rejoindre le point de départ
(voir figure 1.1).
Figure 1.1:
Exemples de valeurs du nombre de rotation, dans le cas de dynamiques périodiques. À gauche : période=3, nombre de tours=1.
À droite : période=7, nombre de tours=2.
|
|
- Si
 est irrationnel, on parle de pseudo-périodicité.
La période
est irrationnel, on parle de pseudo-périodicité.
La période 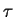 est une valeur réelle irrationnelle.
C'est ce type de dynamique cyclique que l'on obtient lorsque la première bifurcation est une bifurcation de Hopf.
Si l'on regarde de quelle manière les points parcourent le cycle sur l'intervalle d'une pseudo-période, on voit qu'ils décrivent un tour presque complet, au terme duquel ils rejoignent un voisinage du premier point observé.
Ce petit décalage se répercute sur le tour suivant de sorte qu'en fin de compte, si l'on prend suffisamment de points, on voit apparaître la forme du cycle complet (le cycle est densément couvert, voir figure 1.2).
est une valeur réelle irrationnelle.
C'est ce type de dynamique cyclique que l'on obtient lorsque la première bifurcation est une bifurcation de Hopf.
Si l'on regarde de quelle manière les points parcourent le cycle sur l'intervalle d'une pseudo-période, on voit qu'ils décrivent un tour presque complet, au terme duquel ils rejoignent un voisinage du premier point observé.
Ce petit décalage se répercute sur le tour suivant de sorte qu'en fin de compte, si l'on prend suffisamment de points, on voit apparaître la forme du cycle complet (le cycle est densément couvert, voir figure 1.2).
Figure 1.2:
Différentes représentations d'un même signal  .
On a pris pour cet exemple un signal pseudo-périodique
.
On a pris pour cet exemple un signal pseudo-périodique
 (n'oublions pas que
(n'oublions pas que  est discret !).
Le diagramme en haut à gauche donne le signal temporel sur 100 pas de temps.
On a en haut à droite le spectre de puissance de ce signal, sur lequel la fréquence fondamentale est proche de
est discret !).
Le diagramme en haut à gauche donne le signal temporel sur 100 pas de temps.
On a en haut à droite le spectre de puissance de ce signal, sur lequel la fréquence fondamentale est proche de
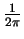 , correspondant à une pseudo-période
, correspondant à une pseudo-période
 .
Le diagramme de premier retour du signal
.
Le diagramme de premier retour du signal  est donné en bas à gauche, tracé à partir de 1000 points de la dynamique.
On voit en particulier que le cycle est densément couvert. En bas à droite, on a représenté 6 points successifs reliés par des lignes. On voit qu'après 6 pas de temps, le point de la trajectoire se retrouve à proximité du point initial.
est donné en bas à gauche, tracé à partir de 1000 points de la dynamique.
On voit en particulier que le cycle est densément couvert. En bas à droite, on a représenté 6 points successifs reliés par des lignes. On voit qu'après 6 pas de temps, le point de la trajectoire se retrouve à proximité du point initial.
|
|
Enfin, la valeur de la période (cas rationnel) ou de la pseudo-période (cas irrationnel) est exactement l'inverse du nombre de rotation.
La plus petite valeur entière supérieure à la pseudo-période nous donne le nombre de pas de temps nécessaires pour faire un tour complet de l'attracteur.





suivant: Exposants de Lyapunov
monter: Outils numériques
précédent: Fonction d'auto-corrélation
Table des matières
Index
Dauce Emmanuel
2003-05-07
![]() , on appelle nombre de rotation
, on appelle nombre de rotation ![]() la quantité
la quantité
![]() , où
, où
![]() est l'angle moyen formé entre des triplets de points successifs de la dynamique, sur toute la trajectoire dans l'espace des phases.
Si
est l'angle moyen formé entre des triplets de points successifs de la dynamique, sur toute la trajectoire dans l'espace des phases.
Si ![]() est mono dimensionnel, le nombre de rotation est également défini dans l'espace de premier retour, auquel cas les coordonnées des points des triplets sont (
est mono dimensionnel, le nombre de rotation est également défini dans l'espace de premier retour, auquel cas les coordonnées des points des triplets sont (![]() ,
, ![]() ), (
), (![]() ,
, ![]() ), (
), (![]() ,
, ![]() ).
).
![\includegraphics[]{nb_rot.eps}](img292.png)
![\includegraphics[]{prelim_sigtemp.eps}](img293.png)
![\includegraphics[]{prelim_spectre.eps}](img294.png)
![\includegraphics[]{prelim_cycle.eps}](img295.png)
![\includegraphics[]{prelim_periode.eps}](img296.png)