suivant: Attracteurs
monter: Systèmes dynamiques
précédent: Systèmes dynamiques
Table des matières
Index
Un système dynamique est défini par un triplet
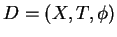 , constitué de l'espace d'états
, constitué de l'espace d'états 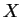 , du domaine temporel
, du domaine temporel 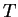 et d'une fonction de transition d'état
et d'une fonction de transition d'état
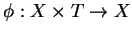 , qui possède la propriété :
, qui possède la propriété :
Pour tout 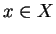 et
et
 ,
,
La fonction  décrit la façon dont le système évolue au cours du temps.
Si cette fonction ne dépend pas du temps, le système est autonome.
La taille de
décrit la façon dont le système évolue au cours du temps.
Si cette fonction ne dépend pas du temps, le système est autonome.
La taille de 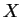 (nombre de variables d'état) est
(nombre de variables d'état) est  .
On l'appelle aussi
.
On l'appelle aussi  l'ordre du système.
l'ordre du système.
Le choix de l'espace temporel 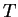 est décisif, et dépend en général du phénomène que l'on souhaite modéliser.
Si
est décisif, et dépend en général du phénomène que l'on souhaite modéliser.
Si
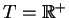 , le système est dit à temps continu, et si
, le système est dit à temps continu, et si
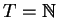 , le système est dit à temps discret.
, le système est dit à temps discret.
- Les systèmes à temps continu servent en général à décrire l'évolution de grandeurs physiques.
Une équation différentielle de type
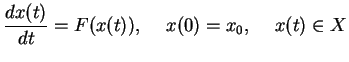 inclus dans inclus dans  |
(1.1) |
permet de définir un système dynamique à temps continu
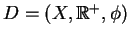 où
où  est la solution de (1.1)
est la solution de (1.1)
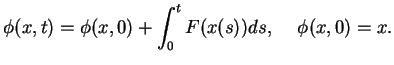 |
(1.2) |
- Le formalisme des systèmes à temps discret est utile, entre autres, pour décrire le comportement des systèmes de traitement de l'information comme les réseaux de neurones.
Il est usuel de définir un système à temps discret à l'aide
d'une application
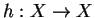 qui définit un système dynamique
qui définit un système dynamique
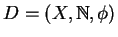 où
où  est donné par des itérations de
est donné par des itérations de 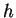 Pour la suite de ce travail, le système étudié sera un système à temps discret, c'est pourquoi nous privilégierons les notations de type temps discret pour décrire les propriétés des systèmes dynamiques.
Pour la suite de ce travail, le système étudié sera un système à temps discret, c'est pourquoi nous privilégierons les notations de type temps discret pour décrire les propriétés des systèmes dynamiques.
Quelques définitions :
- Pour tout
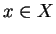 , la trajectoire qui a
, la trajectoire qui a 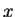 pour origine
est définie par l'application
pour origine
est définie par l'application
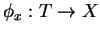 telle que
telle que
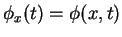 .
Le terme trajectoire est issu de la physique classique dans le cas où les variables d'état sont les coordonnées d'un point matériel dans un espace à 3 dimensions.
Lorsque les variables d'état représentent des grandeurs autres que des coordonnées spatiales, il est néanmoins possible de représenter les trajectoires au sein de l'espace d'état, également appelé espace des phases.
Par ailleurs, on appelle orbite de
.
Le terme trajectoire est issu de la physique classique dans le cas où les variables d'état sont les coordonnées d'un point matériel dans un espace à 3 dimensions.
Lorsque les variables d'état représentent des grandeurs autres que des coordonnées spatiales, il est néanmoins possible de représenter les trajectoires au sein de l'espace d'état, également appelé espace des phases.
Par ailleurs, on appelle orbite de 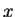 l'ensemble d'états
l'ensemble d'états
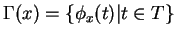 .
.
- À l'instant
 , on définit le flot du système par l'application
, on définit le flot du système par l'application
 telle que
telle que
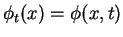 .
Pour les systèmes à temps discret, on a
.
Pour les systèmes à temps discret, on a 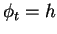 .
.





suivant: Attracteurs
monter: Systèmes dynamiques
précédent: Systèmes dynamiques
Table des matières
Index
Dauce Emmanuel
2003-05-07
![]() , constitué de l'espace d'états
, constitué de l'espace d'états ![]() , du domaine temporel
, du domaine temporel ![]() et d'une fonction de transition d'état
et d'une fonction de transition d'état
![]() , qui possède la propriété :
, qui possède la propriété :
![]() et
et
![]() ,
,
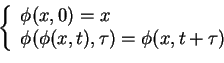
![]() décrit la façon dont le système évolue au cours du temps.
Si cette fonction ne dépend pas du temps, le système est autonome.
La taille de
décrit la façon dont le système évolue au cours du temps.
Si cette fonction ne dépend pas du temps, le système est autonome.
La taille de ![]() (nombre de variables d'état) est
(nombre de variables d'état) est ![]() .
On l'appelle aussi
.
On l'appelle aussi ![]() l'ordre du système.
l'ordre du système.
![]() est décisif, et dépend en général du phénomène que l'on souhaite modéliser.
Si
est décisif, et dépend en général du phénomène que l'on souhaite modéliser.
Si
![]() , le système est dit à temps continu, et si
, le système est dit à temps continu, et si
![]() , le système est dit à temps discret.
, le système est dit à temps discret.