




suivant: Fonction d'auto-corrélation
monter: Comportement dynamique global
précédent: Spectre pour les dynamiques
Table des matières
Index
On a représenté sur la figure 3.9 l'évolution de la la période dominante (l'inverse de la fréquence dominante) sur 8 réseaux de taille 200, pour des valeurs de  comprises entre
comprises entre  et
et
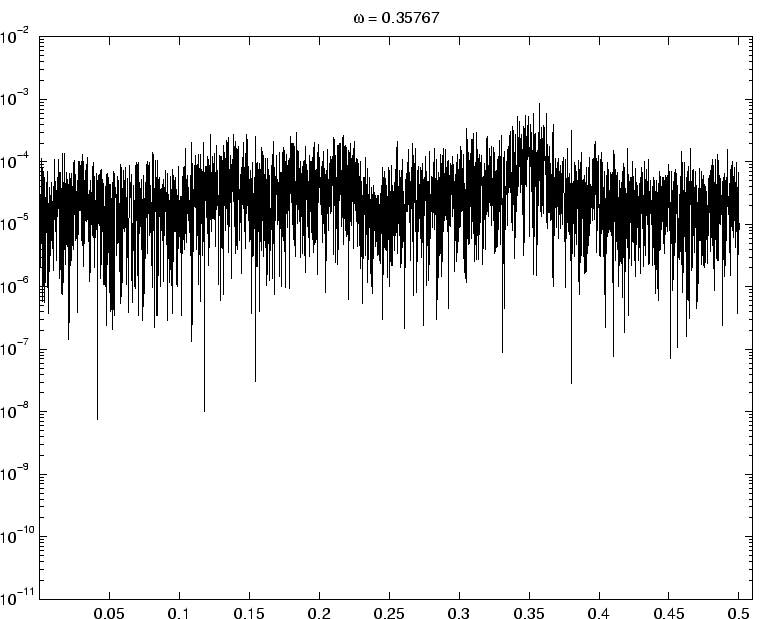 .
On constate sur ces 8 réseaux que
la période dominante se maintient à la même valeur sur une plage correspondant à la route vers le chaos. Suite à l'entrée dans le chaos, le spectre tend à devenir de plus en plus uniforme et d'autres périodes (correspondant souvent à d'autres harmoniques de la fondamentale) peuvent prendre le dessus.
.
On constate sur ces 8 réseaux que
la période dominante se maintient à la même valeur sur une plage correspondant à la route vers le chaos. Suite à l'entrée dans le chaos, le spectre tend à devenir de plus en plus uniforme et d'autres périodes (correspondant souvent à d'autres harmoniques de la fondamentale) peuvent prendre le dessus.
Figure 3.9:
Évolution de la période dominante après la déstabilisation pour 8 réseaux.
Pour chaque réseau, on regarde la valeur 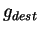 de déstabilisation, et on regarde la période dominante pour
de déstabilisation, et on regarde la période dominante pour
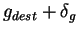 , avec
, avec
 .
La valeur de
.
La valeur de 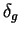 est en abcisse, et la valeur de la période en ordonnée (chaque ligne pleine correspond à un réseau différent).
On notera que les deux lignes corespondant à la période 2 (bifurcation flip) se superposent.
Paramètres :
est en abcisse, et la valeur de la période en ordonnée (chaque ligne pleine correspond à un réseau différent).
On notera que les deux lignes corespondant à la période 2 (bifurcation flip) se superposent.
Paramètres :  ,
,  ,
,
 ,
,
 ,
, 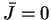 ,
,
 .
.
|
|





suivant: Fonction d'auto-corrélation
monter: Comportement dynamique global
précédent: Spectre pour les dynamiques
Table des matières
Index
Dauce Emmanuel
2003-05-07
 .
On constate sur ces 8 réseaux que
la période dominante se maintient à la même valeur sur une plage correspondant à la route vers le chaos. Suite à l'entrée dans le chaos, le spectre tend à devenir de plus en plus uniforme et d'autres périodes (correspondant souvent à d'autres harmoniques de la fondamentale) peuvent prendre le dessus.
.
On constate sur ces 8 réseaux que
la période dominante se maintient à la même valeur sur une plage correspondant à la route vers le chaos. Suite à l'entrée dans le chaos, le spectre tend à devenir de plus en plus uniforme et d'autres périodes (correspondant souvent à d'autres harmoniques de la fondamentale) peuvent prendre le dessus.