Fonction d'auto-corrélation

Figure 3.10: Autocorrélation du signal moyen $m_N(t)$, pour des valeurs de $g$ croissantes en régime chaotique. La valeur de $\tau$ est en abcisse, celle de $\psi (\tau )$ en ordonnée, avec de gauche à droite $g=7.02$ (frontière du chaos), $g=7.2$, et $g=8$ (chaos profond). Paramètres : $T=500$, $N=200$, $\bar{\theta}=0.1$, $\sigma _\theta =0.1$, $\bar{J}=0$, $\sigma _J=1$.

Dans nos systèmes, ou la dynamique chaotique conserve une périodicité résiduelle vers la frontière du chaos, il subsiste une mémoire des états passés, dans la mesure où la valeur de $g$ n'est pas trop éloignée de la frontière du chaos.

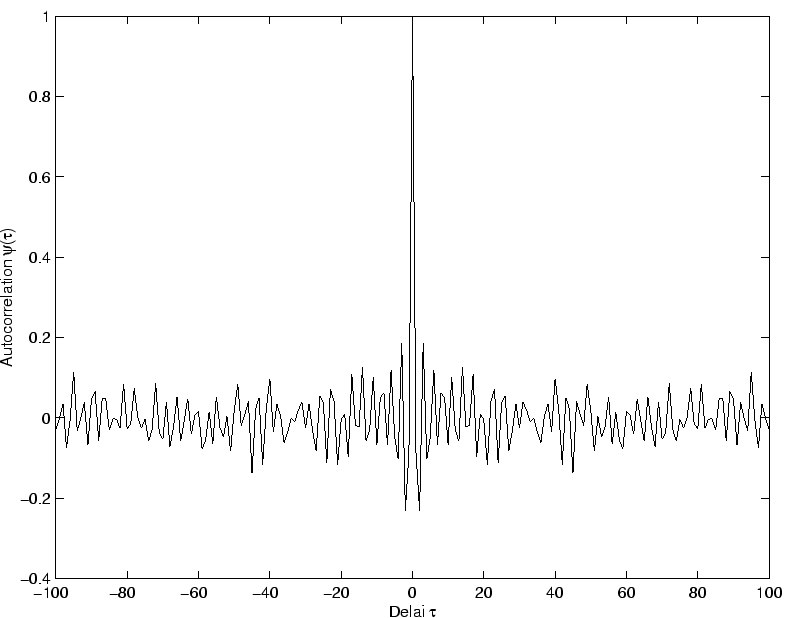
Sur la figure 3.10, on a représenté la fonction d'auto-corrélation (définie page ), pour des valeurs de $g$ allant de la fontière du chaos au chaos profond (qui peuvent être mis en correspondance avec les spectres de puissance de la figure 3.8). On constate que plus la dynamique chaotique correspond à des valeurs de $g$ éloignées de la frontière du chaos ( $g_{chaos}\simeq 7$ sur ce réseau), plus la fonction d'autocorrélation tend à décroître (en moyenne) avec $\tau$. Cela indique que plus on s'enfonce dans le chaos, plus le réseau tend à perdre la mémoire de ses états passés. Pour $g=8$, qui correspond à un chaos profond sur ce réseau, la fonction d'auto-corrélation est similaire à celle d'un signal aléatoire. Le réseau perd quasiment toute mémoire de ses états passés.

Le résultat le plus important de cette approche par transformée de Fourier est que la fréquence dominante reste la même sur une plage de valeurs de $g$ qui va de la déstabilisation jusqu'au chaos profond. Sur cette plage, la dynamique du réseau est ``rythmée'' par la même pulsation de base. Ainsi, la période qui se met en place à la déstabilisation est loin d'être anecdotique, puisqu'elle conditionne la nature de la dynamique du réseau pour une large plage de valeurs de $g$.

On a vu dans les sections précédentes que cette période fondamentale est intimement liée aux caractéristiques de la jacobienne à la déstabilisation, qui elle même est conditionnée par la configuration spatiale des activations du réseau. On constate ici la persistance du lien entre configuration spatiale et périodicité de la dynamique.