Répartition des périodes en dynamique contrainte

On a vu (section 3.1.4) qu'un motif statique modifie profondément la configuration spatiale des activations, qui conditionne à son tour la configuration du spectre de la jacobienne à la déstabilisation. La justesse de l'approximation selon laquelle la probabilité d'apparition d'une valeur propre formant un angle $\alpha$ avec l'axe des réels est uniformément répartie sur $[0,\pi]$ a pu être constatée lorsque cette mesure est effectuée sur un grand nombre de réseaux différents (voir figure 3.5).

Cette répartition est maintenant mesurée sur un seul réseau, auquel on présente de nombreux motifs différents. Sur un réseau donné, de taille $N=200$, 1000 motifs gaussiens tirés indépendamment selon $\bar{I}$ et $\sigma _I$, sont successivement présentés. Le choix des valeurs $\sigma _I=0.3$, $\bar{I}=-0.4$ assure que la modification induite sur la configuration spatiale est significative et spécifique pour chaque motif différent (voir section 3.1.4). La répartition obtenue est présentée sur la figure 3.24.

Figure: Répartition empirique des périodes en dynamique contrainte.Cette répartition est issue d'une mesure sur 1 réseau, auquel on a présenté 1000 motifs différents définis selon les paramètres $\bar{I}=-0.4$, $\sigma _I=0.3$. On a tracé en pointillé la densité théorique $f(x)=2/{x^2}$. Paramètres : $N=200$, $\bar{\theta}=0$, $\sigma _\theta =0$, $\bar{J}=0$, $\sigma _J=1$.

On voit la grande proximité entre la répartition des périodes issue de 1000 réseaux différents (voir figure 3.5), et celle issue de 1000 motifs différents sur un seul réseau (figure 3.24). Cette dernière présente néanmoins une surdensité plus accentuée pour les périodes proches de 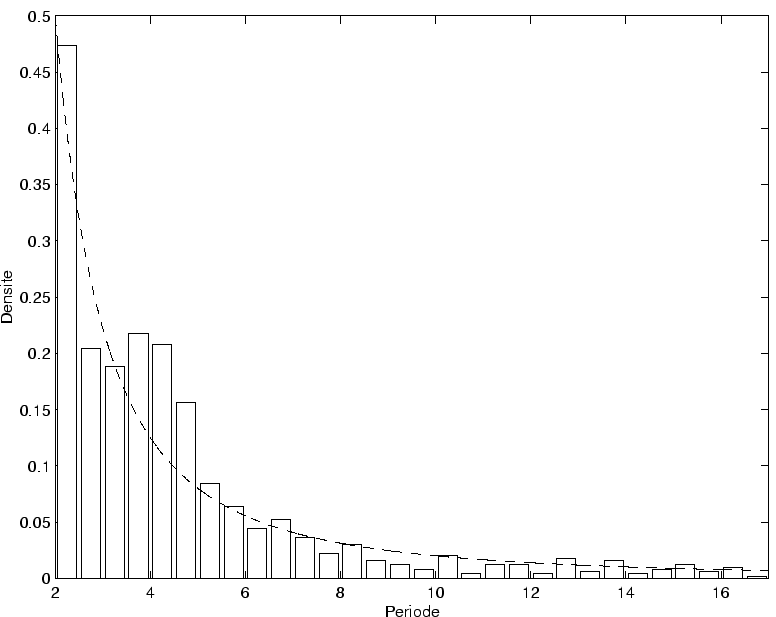$4$.

Il a par ailleurs été vérifié que des répartitions analogues se retrouvent sur tout réseau défini selon les mêmes paramètres.

Sachant qu'à chaque période correspond une organisation sous-jacente sous forme de circuit d'activation, on voit que l'organisation dynamique s'adapte au motif, et à chaque motif différent on peut asocier une organisation dynamique différente. Le système semble pouvoir se reconfigurer à l'infini, et adapter son organisation interne aux circonstances. Le système apparaît comme très malléable.