Régimes cycliques

Dès lors que 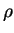$\rho$ dépasse la valeur 1, le système est dit déstabilisé. On a une bifurcation, et on entre dans un nouveau régime dynamique.

Le dépassement de la valeur 1 signifie qu'une des dimensions du système n'est plus contractante, et selon cette direction, la distance entre deux trajectoires tend à augmenter. Le système est dilatant selon cette direction. Le système étant non-linéaire, la distance atteint une valeur limite dictée par les termes de second ordre.

La nature de ce nouveau régime dynamique dépend des caractéristiques de la valeur propre maximale de la jacobienne. Du fait de la non-symétrie des connexions, ces valeurs propres prennent leurs valeurs sur l'espace complexe 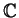$\mathbb{C}$. On voit donc naturellement se dessiner trois cas:

• Si la valeur propre est réelle, égale à 1. On a alors une bifurcation de type n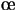ud-col. Il y a apparition d'un nouveau point fixe stable, et le précédent point fixe devient instable. Dans ce cas, Il n'y a pas déstabilisation au sens d'apparition d'une oscillation. On constate néanmoins que ce type de bifurcation est extrêmement rare sur notre modèle. L'étude de la figure 2.7 montre d'ailleurs que le spectre est moins dense aux alentours de la valeur réelle 1. Il est difficile de proposer une explication à ce phénomène : purement numérique ou plus profond ?
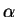• Si la norme maximale est atteinte par deux valeurs complexes conjuguées (cas le plus courant), on a une bifurcation de Hopf. C'est la bifurcation la plus commune. Le système atteint un régime périodique ou semi-périodique, dont la pseudo-période est donnée par $2\pi/\alpha$ où $\alpha$ est l'angle entre la demi-droite centrée qui passe par cette valeur propre et l'axe des réels (voir figure 2.9).
• Si la valeur propre est réelle, égale à -1. On a une bifurcation flip. Le nouveau régime dynamique est périodique, de période 2.

La répartition radiale des valeurs propres approchant une répartition uniforme sur le disque complexe de rayon 1, on s'attend à a voir presque sûrement une bifurcation de Hopf (voir à ce titre [78]). Il s'avère que du fait de la surdensité sur l'axe des réels, les bifurcations flip, bien que moins courantes, ne sont cependant pas rares pour des valeurs de $N$ de l'ordre de 100.

La figure 2.9 donne un exemple de spectre de jacobienne atteint à la déstabilisation sur un réseau de taille 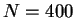$N=400$, ainsi que la dynamique cyclique atteinte après bifurcation.

Figure 2.9: La figure de gauche représente le spectre de la jacobienne du système dans l'espace complexe (axe des réels, axe des imaginaires) à la valeur de déstabilisation 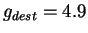$g_{dest}=4.9$. Deux valeurs propres conjuguées franchissent la valeur 1, et forment avec l'axe des réels un angle 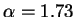$\alpha =1.73$ ce qui donne une pseudo-periode de l'ordre de 3.63. La figure de droite donne la carte de premier retour de la dynamique stationnaire, pour un paramètre de gain légèrement supérieur $g=4.95$. La dynamique est cyclique, avec une pseudo-période de l'ordre de 3.61. Six points successifs de la dynamique sont reliés par des lignes. On constate qu'il faut un peu plus de trois et un peu moins de quatre itérations pour ``faire le tour'' de l'attracteur. Le système a été défini avec les paramètres $N=400$, $\bar{\theta}=0.1$, $\sigma _\theta =0.1$, $\bar{J}=0$, $\sigma _J=1$.

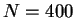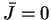Pour la suite on appellera régimes cycliques les régimes périodiques ou pseudo-périodiques. Dans ce cas, le terme cyclique s'oppose au terme chaotique.